AlN在α-Al2O3(0001)表面吸附过程的理论研究

　　采用基于密度泛函理论的平面波超软赝势法,对α-Al2O3 (0001) 表面吸附AlN 进行了动力学模拟计算,研究了AlN分子在a-Al2O3 (0001) 表面吸附成键过程、吸附能量与成键方位。计算表明吸附过程经历了物理吸附、化学吸附与稳定态形成的过程,其化学结合能达到4.844eV。吸附后AlN 化学键(0.189 ±0.010nm) 与最近邻的表面Al - O 键有30°的偏转角度,Al 在表面较稳定的化学吸附位置正好偏离表面O 六角对称约30°,使得AlN 与蓝宝石之间的晶格失配度降低。

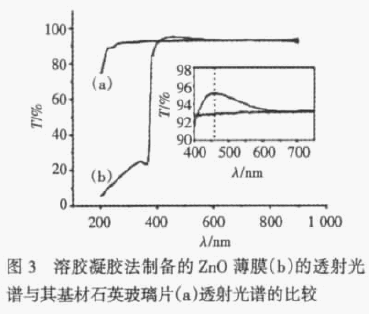
　　α-Al2O3 ,又称刚玉,广泛地用作制备AlN、ZnO等电子薄膜半导体材料的基片。蓝宝石基片上生长AlN 薄膜在微电子、电子元件、高频宽带通信以及功率半导体器件等领域具有应用前景。其中采用分子束外延(MBE) 、激光脉冲沉积(PLD)  、射频磁控溅射沉积(MRS)  、微波等离子辅助溅射、溶胶-凝胶(solgel) 、金属有机化学气相沉积(MOCVD)  、激光分子束外延(LMBE) 、激光化学气相沉积(LCVD) 等真空技术生长的AlN 薄膜质量较高。

　　在这方面,关于AlN 薄膜在α-Al2O3 (0001) 基底上的制备方法与生长特性有较多的实验研究报导,而对AlN 薄膜在α-Al2O3 (0001) 表面的最初生长机理尚缺乏理论计算研究。

　　在真空中,采用外延生长法制备薄膜的生长过程中,首先基片的表面结构、缺陷等强烈地影响薄膜生长的模式、形貌以及界面特性,从而对薄膜材料的功能起到决定性作用。再有,沉积粒子在基片表面吸附、扩散、结合,对成核和生长初期阶段的性质有非常重要的影响,并直接影响着将要形成的整个薄膜的质量。由于表面实验分析技术对表层原子结构、表面键合与表面电荷、表面吸附以及表面势能等方面的研究仍然缺乏充分的实验研究,尤其是对杂的氧化物表面。因此运用可靠的理论计算研究晶体表面、及其表面的化学与物理吸附,已成为一种重要的晶体表面研究方法。

　　为了减小失配度而提高AlN 薄膜的质量已经做了大量的研究 。从理论上来讲,AlN 与蓝宝石在c 轴上的晶格失配度非常大(61.11 %) ,但实验报导AlN 仍然可以在蓝宝石基底上生长,这是由于通过物理方法使得AlN 先成核,然后再吸附在基底上面或者是先让GaN 等做一个缓冲层,然后再吸附。同时董树荣在FBAR 用AlN 薄膜的射频反应溅射制备研究一文中也提出了AlN 薄膜可以均匀的沿c 轴堆垛生长。然而,到目前为止,在实验上还无法从原子尺度上获得粒子吸附生长过程的微观动态信息,如基底表面物理、化学吸附生长的过程,以及粒子最初在表面的吸附位置以及运动轨迹。因此对这些方面,有必要进一步研究。<

　　本文主要目的是研究AlN 单分子在α-Al2O3(0001) 表面的吸附,内容安排如下:第1 节简要介绍了物理模型与计算方法,第2 节重点论述并讨论了AlN 的吸附过程与表面结构,最后第3 节进行了总结。

1、物理模型与计算方法

　　我们知道,AlN 在α-Al2O3 (0001) 表面扩散、吸附位置及键合作用关系到AlN 粒子簇小岛进一步的形成,影响AlN 薄膜的生长。因此研究分析AlN 在基底表面的吸附过程与成键特性,对研究AlN 薄膜生长初期的机理有非常重要的意义。α-Al2O3 (0001) 表面的原子与表面电子态对外来粒子的吸附直接相关,为此, 我们首先有必要得到一个已弛豫的α-Al2O3 (0001) 表面,分析其表面原子与电子结构,进一步构造AlN 的吸附模型。

　　对AlN 的吸附模型,基片采用文献报导已优化的超晶胞6 个原子层的slab 表面(2 ×1) 模型,表面终止原子为单层Al 的表面结构。为了观察AlN 分子中的N 和Al 同基片表面的Al 、O 结合先后过程,我们将优化得到的气态AlN 分子(键距0.185nm) ,水平置入基片上空,距离基片表面013nm,充分考虑了真空区高度较小对计算的影响, 因此真空层设置为210nm,如图1(a) 。其中考虑了表面吸附位置、吸附分子结构和空中下落的方位。为了表述方便,AlN 分子中的N 同表面的Al 结合表示为(Al)N - Al ,其Al 同基片表面的O 结合,表示为Al - O(基片) 。

　　α-Al2O3 (0001) 基片表面原子结构为氧6 重对称结构,为了考察表面主要吸附位置,设定了8 个不同的主要吸附位置 ,这些位置实际上可以看作是AlN 薄膜的最初生长点,见图1 (b) 。在(2 ×1) 的吸附模型图1 中,我们仅考虑了AlN 分子水平从空中落下的两种情况。一是模型A:Al 、N 分别位于吸附位S7 和S6 上空,如图1(c) 所示,AlN 分子中的Al与表面两个Al 距离相等,而N 距离表面Al ②较近。另一种情况相反,如图1 (d) 模型B 所示,N 与表面两个Al 距离相等,而AlN 分子中Al 距离表面Al ②较近。吸附模型A 与模型B 用于观察AlN 分子中的Al 和N 距离表面A1 远近对表面吸附的影响。

　　图1 　AlN/ a-Al2O3 (0001) 表面吸附位置与AlN 吸附模型(a) 薄片吸附模型, (b) 顶层不同吸附位置, (c) 吸附模型A , (d) 吸附模型B。　图中灰色小球代表基片O 原子,标为O2 ;黑色小球代表基片Al 原子;较大的黑色球代表基片表面的两个Al 原子,分别标记为Al ①和Al ②;较大的灰色球代表基片O 原子,标记为O1 ;白色小球代表N 原子,较大的深灰色小球代表AlN 中的Al 原子。

　　我们采用基于密度泛函理论( density functionaltheory ,DFT) 总能量赝势法,由CASTEP(cambridge se2rial total energy package) 软件包实现计算。运用D.Vanderbilt 提出的超软赝(ultrasoftpseudopotentials ,USP) 来描述离子实与价电子之间的相互作用(O 2s22 p4 ,Al 3 s23 p1 ,N 2 s22 p5) 。对电子交换相关项的计算选择了Perdew 等提出的广义梯度近似(general gradient approximation ,GGA) 修正方法(PW91) 形式。通过前面总结分析α-Al2O3 (0001) 表面的计算,我们知道运用密度泛函理论,相对于结合能的计算来说,在计算键长与几何构形时,对计算条件相当不敏感,电荷密度分布随计算条件的变化相当小,相对均方差在10 ^{- 4}量级,特别对于数值积分点数不敏感 。为了适当减小动力学的运算量,在采用超软赝势计算时,可以适当减小截断能Ecut的取值,我们取截断能量Ecut为340eV。在对2×2 表面结构的优化中,采用了BFGS 算法(Broyden Fletcher Goldfarb and Shanno ,BFGS) ,布里渊区k2point 取的是3 ×3 ×2 ,即18 个K-point 。对2 ×1 表面AlN 的吸附动力学模型,我们运用了CASTEP 软件包中的动力学程序布里渊区k-point 取的是5 ×2 ×1 ,即10 个k-point ,积分时间步长设为1.0 fs ,模拟总时间为1.5ps ,体系温度恒定为500 ℃。通过对α-Al2O3(0001) 表面结构优化与弛豫计算,以及对AlN 分子键长、键能试算,结果都非常好地吻合于文献值 ,同时与Gauss98 软件包所计算的AlN 键长值(0.170nm) 也非常一致,表明我们计算结果是可靠的。