平面磁控溅射薄膜厚度均匀性的研究概述

　　在平面磁控溅射镀膜系统中，薄膜厚度均匀性作为衡量薄膜质量和成膜系统性能的一项重要指标，得到了国内外学者们的广泛研究。本文以膜厚分布的理论模型为出发点，从工艺条件及模型参数两个方面，对靶与基片的位置关系、基片的运动方式、靶材的形状、溅射功率、工作气压、工作模式等各种影响以及改善薄膜厚度均匀性的因素进行了系统的归纳和陈述。最后对平面磁控溅射镀膜系统膜厚分布的研究进展进行总结并提出了展望。

　　早在20 世纪30 年代中期，薄膜应用已遍及国民经济的各个领域。薄膜技术主要包括薄膜的制备技术和薄膜材料的研究，薄膜的制备技术又称为镀膜技术。在各种溅射镀膜技术中，磁控溅射技术是最重要的物理气相沉积方法之一，它在等离子体产生、维持以及效率方面与其他技术相比都有了很大的改进，较易获得沉积速率更高，致密性与结合力更好的薄膜，因此在机械、光学和电子行业得到了广泛的应用。然而，该系统下靶材的利用率比较低，通常低于30%，沉积速率和薄膜厚度均匀性是影响薄膜性能的重要因素，也直接影响了薄膜器件的功能。近三十年来，为了研究磁控溅射镀膜系统膜厚分布情况，相关领域研究人员进行了大量的工作。

　　根据上述文献，本文对平面磁控溅射薄膜厚度的理论计算模型进行了阐述，根据改善膜厚均匀性的手段进行了分类和讨论：从实验条件方面改善工艺条件包括改变靶基距、溅射功率以及工作气压等；理论基础方面分别通过改变靶与基片的位置关系、靶材的形状、基片的运动方式、膜厚分布的算法等方面因素，其中靶与基片的位置关系包括靶与基片的距离、靶与基片的角度关系，靶材形状分为圆形和矩形以及不规则形状等，基片的运动方式包括纯自转系统和公自转系统两种情况，计算膜厚分布的方法分为积分和有限元网格划分两种算法；最后讨论了沉积过程对膜厚均匀性的影响，沉积过程的研究主要基于Monte- Carlo 模型和流体模型进行求解。下面首先提出计算所需的物理和数学模型，然后以模型为出发点，分节对各种方法进行深入讨论。

1、磁控溅射膜厚计算的数学模型

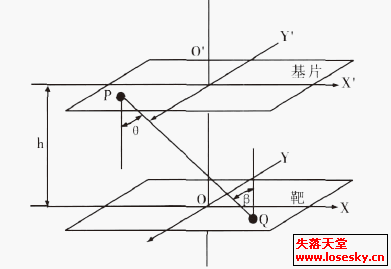
　　对于膜厚分布计算公式的研究，基本模型为基片与靶平面平行，如图1 所示，图中阴极靶与基片的垂直距离为h。设P 为基片上任一点，其坐标为(x, y)。ds 为P 点的微小面元。Q 为溅射跑道区内一点(x', y')，dσ 为Q 点的微小面元。由X. Q. Meng，Gnaedinger 等人阐述，此类平面磁控溅射镀膜系统膜厚分布的讨论是建立在下面4 个假设的基础上的：

　　① 假定溅射离子是垂直入射到靶面的，离子入射角为0。

　　② 由于在跑道区域内部磁场最强，且二次电子和高度离化的气体分子被紧紧束缚在里面，因此假设溅射过程中的刻蚀现象仅仅发生在跑道上，圆形靶（刻蚀环半径r1~r2 之间），矩形靶（矩形环内部）。

　　③ 认为被溅射出来的薄膜原子离开靶面的角度分布为余弦指数分布。

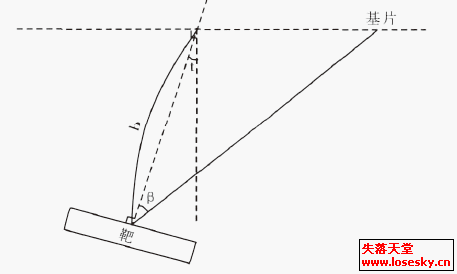
图1 平行同轴平面磁控溅射示意图　　图2 倾斜非同轴平面磁控溅射示意图

3、结束语与展望

　　平面磁控溅射沉积薄膜厚度均匀性的影响因素很多，本文对靶- 基距、基片运动方式、靶材形状、磁控溅射内部磁场和刻蚀情况等方面原因进行研究和概述。得出以下几点结论：

3.1、工艺方面

　　调整工艺参数可以改善膜厚的均匀性，比如增加靶- 基距，增加溅射功率、适当的增加腔体气压，膜厚分布均匀性在一定程度上有提高的趋势。

3.2、理论模型方面

　　（1）比较了共轴与非共轴两种情况的平面磁控溅射镀膜系统，对于倾斜非同轴平面磁控溅射，可以求解出最优的倾斜角与倾斜位移使得膜厚分布更加均匀。

　　（2） 靶材形状的不同，直接改变了相对厚分布的积分形式。通过在靶上挖孔和增加挡板的方法也可以调整膜厚均匀性。

　　（3）基片的运动方式也是膜厚分布的重要影响因素，其中公- 自转磁控溅射镀膜系统可以提高溅射效率，薄膜厚度均匀性与公- 自转角速度比例有直接关系。

　　（4）沉积过程对膜厚分布有重要的影响，其中包括将蒙特卡罗和流体两种模型结合起来对磁控溅射内部等离子体能量和运动机理的模拟。

　　（5）对于其他的磁控溅射系统，例如平衡与非平衡两种工作模式，由于磁场分布不同，膜厚均匀性影响因素也不同。

　　理论模型的计算和分析是工艺优化的基础，为了更加精确地研究膜厚度的分布情况，讨论沉积过程中的等离子体放电和运动情况则更为重要。总的来说，对于平面磁控溅射镀膜系统膜厚均匀性的讨论需要从以下三个方面努力，一方面是对物理过程的深刻理解，建立物理模型，第二个方面是对物理过程的合理近似，建立可以在有限条件下求解的数学模型，第三方面是实验和工艺方面的具体实施。应该说，一般科学或工程上的问题都可以通过上述三个过程来进行定性和定量的分析，理论结合实验研究，构成解决问题的完美模式。然而，对于磁控溅射装置的膜厚控制，无论理论研究还是实验研究，都远远不够，需要广大的科技工作者继续努力。