磁控过程的计算机模拟

　　本文基于蒙特卡罗方法，并结合SRIM软件，编制程序跟踪模拟了磁控溅射各物理过程的粒子状态。以铝靶材为例，得到了粒子在磁控溅射各物理过程的状态分布，讨论了工作参数对薄膜沉积过程的影响。模拟结果表明：溅射原子的能量主要分布在20 eV 以下，当原子沉积到基片表面时，其能量主要分布在15 eV 以下，但有两个分布峰值，两个分布峰值对应着快慢两种不同形式的沉积过程。原子沉积到基片表面的位置大致服从正态分布，气压p 和靶基距离d 影响正态分布的方差，也即影响沉积原子在基片表面分布的均匀性。功率与沉积速度呈良好的线性关系，在工作气压为1 Pa，靶基距离为60 mm 的条件下，当入射粒子的能量为250 eV 时，模拟得到的功率效率最大。

　　磁控溅射技术由于具有溅射原子能量高、薄膜附着力大、成膜致密性好等优点，被广泛用于各种材料薄膜的制备。膜的沉积速率和膜的均匀性与气体压强、溅射功率等工作参数有关。很多学者从理论上和实验上分析了工作参数对磁控溅射的影响，但由于磁控溅射中各部分物理过程在空间和时间尺度上跨度较大，且包含了大量的随机过程，单纯的理论分析会显得十分困难。随着计算机技术和数值计算方法的发展，使得用计算机对磁控溅射各物理过程的粒子模拟和跟踪已成为可能。蒙特卡罗方法是一种具有独特风格的数值计算方法，在求解随机性问题时独具优势。本文基于蒙特卡罗方法，编制程序模拟了磁控溅射的各物理过程，并以铝靶为例，讨论了工作参数对磁控溅射各过程的影响。模拟方法和结果对磁控溅射的理论研究和实验工作有一定的参考意义。

1、模型与假设

　　（1）系统处于动态平衡。在一定的工作参数下，靶电流稳定，电流密度在靶面均匀分布。工作气体服从麦克斯韦速率分布。入射离子和溅射原子相对工作气体而言数量很少，除了与工作气体产生碰撞外，不发生其它相互作用。

　　（2）入射离子的加速电压近似看做壳层与阴极的电势差。由于离子质量较大，可认为磁强对离子的运动基本没有影响。入射离子在电场的作用下，垂直入射靶面。

　　（3） 模拟参数设置如下：工作气体为氩气，靶材半径为30 mm。真空腔半径为100 mm，即当被跟踪的溅射原子的水平半径大于100 mm 时，认为原子被真空腔吸收，结束模拟。在求平均自由程时，有效碰撞直径取氩气的范德瓦斯直径，其值为3.82 魡。铝的晶格常数取4.05 魡。

2、分析与计算

2.1、磁控溅射过程的分析和模拟软件的编制

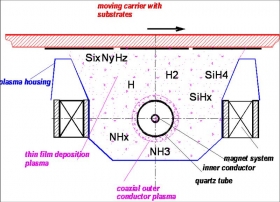
　　磁控溅射一般可分为四个主要的物理过程：辉光放电、入射粒子与靶材的相互作用、溅射原子从靶面到基面的输运过程、溅射原子在基片表面成膜的微观过程。

　　（1）在考虑辉光放电时，我们认为入射粒子是均匀产生的，且由于阴极壳层厚度相对于粒子的平均自由程而言较短，粒子在从壳层向靶面的运动过程中，可认为不与工作气体发生碰撞。入射粒子的方向与靶面垂直，能量即为阴极壳层电压提供给粒子的能量。入射粒子的状态（位置、能量、方向）用MATLAB 模拟生成。

　　（2） 在模拟入射粒子与靶材的相互碰撞作用时，我们用SRIM[4]软件中的TRIM 程序来模拟计算。把生成的入射粒子状态参数作为TRIM 初始数据，经过TRIM 的模拟计算后，可以得到溅射原子的状态。

　　（3）溅射原子输运模拟软件的编制。基于蒙特卡罗理论，编制程序模拟了溅射原子从靶面向基面的输运过程。程序模拟了溅射原子与工作气体的每次随机碰撞，并记录了每次碰撞的位置和碰撞后溅射原子的速度（包括大小和方向），直至所跟踪的溅射原子到达基面或被腔壁吸收，最后可得到溅射原子沉积到基面时的状态。程序设置了三个可调的输入参数（sta，p，d）。sta 包含溅射原子刚从靶面出射时的状态和数量， 可通过TRIM 模拟得到，p 和d 分别代表工作气体的压强和靶基之间的距离。输入三个参数后，运行程序，就能模拟相应工作参数下的溅射原子输运状态。

3、结论

　　跟踪模拟了磁控溅射各物理过程中的粒子状态，得到了粒子在各物理过程的状态分布，并讨论了工作参数对沉积过程的影响。模拟结果表明：

　　（1）任意溅射原子沉积到基片上的位置服从正态分布，正态分布的期望为靶材原子溅射位置沿溅射方向的延长线与基片的交点位置，正态分布的方差与工作气压p 和靶基距离d 有关，p和d 越大，正态分布的方差越大，说明p 和d 越大，原子沉积到基片上时分布得越均匀。

　　（2） 溅射原子的能量主要分布在20 eV 以下，溅射原子的出射方向与靶面法线夹角的余弦主要分布在- 0.8 以下，这说明原子大致是垂直靶面出射的。

　　（3）原子沉积到基面时，其入射方向与基面的法线夹角的余弦主要分布在- 0.5 以下。沉积到基面的原子主要分布在15 eV 以下，但有两个分布峰值。一个分布峰值在1 eV 以下，另一个分布峰值在5 eV 左右。两个分布峰值对应着快慢两种不同状态粒子的沉积。

　　（4）沉积速率与功率呈良好的线性关系，在工作气压为1 Pa，靶基距离为60 mm 的条件下，当入射粒子的能量为250 eV 时，模拟得到的功率效率最大。