磁控溅射带电粒子的运动分布以及靶面刻蚀形貌的研究

　　首先使用有限元分析方法求解磁控溅射电磁场的分布，然后结合受力分析，仿真了单电子运动轨迹并较好地呈现螺旋形状，同时模拟出多粒子束的靶面位置分布以及刻蚀形貌图，最后把计算结果与实验中靶面刻蚀形貌进行对比，所求结果与实验测量数据吻合。

　　在各种溅射镀膜技术中，磁控溅射技术是最重要的技术之一，它在等离子体产生、维持以及效率方面与其他技术相比都有了很大的改进，较易获得高的沉积速率，致密性与结合力更好的薄膜，因此在机械、光学和电子行业得到了广泛的应用。近些年来，关于磁控放电的理论得到广泛的研究，主要包括磁场结构的分析以及物理机制讨论。在磁场放电区域，电子被限制在磁力线平行于阴极表面的位置，从而产生出高电离化的背景气体。在这个区域产生的离子被加速运动的过程中，又会受到电子和离子的碰撞同时产生出二次电子来维持放电。在磁控溅射系统中，由于特殊的磁场结构，靶材表面的磁场分布以及离子分布是不均匀的，从而导致刻蚀的不均匀性，这对于靶的利用率是一个极大的限制，因此针对于靶面粒子分布以及刻蚀形貌的研究具有很重要的指导意义，而最有效的方法就是通过计算机建立模型仿真。

1、计算方法

1.1、电磁场分布的计算

　　平面磁控溅射系统结构如图1所示，图中靶基距为30mm，阴极加-300V偏压，阳极接地，选取铝为靶材，直径为100mm，溅射气体选择氩气。为模拟靶材上方X 与Y 方向的磁场分布以及Y 方向的电场分布，利用有限元分析软件ANSYS 针对上述模型进行求解。磁场与电场分别由公式（1）和（2）表示

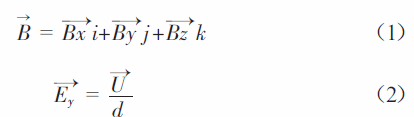
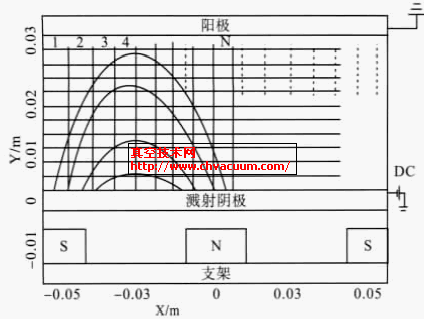
图1 平面磁控溅射示意图

1.2、单电子运动的模拟

　　设粒子的电荷为q，运动速度可以表示为：

　　粒子受到电场力和磁场对它的洛伦兹力的共同作，满足运动方程（4）

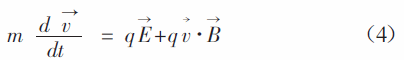
　　速度可以通过上式进行求解，位移表示成方程组（5~7）

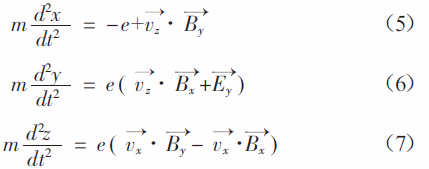
1.3、靶面粒子束流的分布

　　对粒子分布的求解算法如图2 所示。针对电子，首先从X=[-50mm，50mm]，Y=[-30mm，30mm]的区域内任意选定N 个电子，通过前面的电磁场分布可以得到每个电子受到的电场力与磁场力，判断如果电子在所规定的区域内部，则开始运行程序，设定时间步长dt，计算电子在每个时间步长内三个坐标方向上速度与位移的改变量，判断位移改变是否大于电子运动的平均自由程λ，电子自由程指电子在两次碰撞之间运动的平均距离。假设气体层的厚度是dx，密度为n，r表示气体原子的半径，单成分气体中，平均自由程表示为

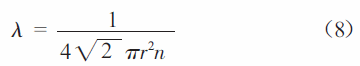
　　如果位移改变大于λ，则有碰撞发生，碰撞后粒子的能量由公式（9）表示

　　此时如果不产生新电子，碰撞为弹性碰撞，满足动量守恒定理；如果产生新电子，碰撞为非弹性碰撞。新电子速度大小和方向服从随机数分布，生成随机数C=rand[0,1]，三个方向的速度大小如公式（10~12）所示

　　最后把电子经过dt时间的运动后的位置分布图绘制出来，对于离子分布的求解与电子算法相同，只是离子受到的电场力方向与电子相反，在这里就不具体陈述了。

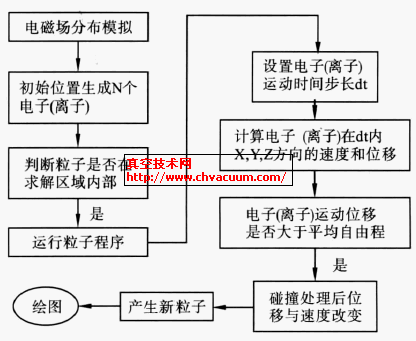
图2 粒子分布算法

1.4、靶面刻蚀形貌

　　如图1 所示，将靶材表面区域内的磁场从起点沿靶材的水平和竖直方向划分为N*N 个网格。将靶材表面第i 个等分点处的疏密程度映射为溅射坑的深度Depth(i)

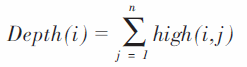
　　其中，high (i,j) 为P 点与靶材间的距离，n为第i个等分点处磁力线的条数。