基于非稳态传热过程的真空玻璃性能建模

　　由于真空玻璃的导热系数测量复杂，本文提出一种基于非稳态传热过程的软测量表征真空玻璃导热系数的模型。首先，在连续介质与半无限大物体的前提下，采用能量守恒定律与拉普拉斯变换法，对数学物理模型进行求解，建立非加热面的中心温度计算公式。然后，利用数值仿真软件FLUENT 对物理模型进行温度场仿真。

　　仿真结果表明：检测时间少于5 分钟，达到节约时间的目的；为保证温度测量准确，取多个测量点的测量值；为减小测量误差，采用圆形加热片时，加热片的半径与真空玻璃厚度之比要大于3。这些为后续研究真空玻璃导热系数与温度变化之间的关系奠定一定的理论和应用基础，对实验有指导意义，为真空玻璃导热系数的在线检测和其过程的优化控制提供指导。

　　在推进节能型社会建设的进程中，建筑节能是不能忽视的重要方面。门窗耗费的能量不容小觑。具有自主知识产权的真空玻璃是一种性能优异的新型节能建材，在全社会节能减排的趋势下，受到了人们的广泛关注。使用真空玻璃门窗后，不仅明显节省了空调的制热制冷费用，极大地提高了居室环境的舒适度，而且由于真空玻璃结构上的特点，即真空层的存在，阻隔了声音的传递，可保持室内宁静空间，减小噪声污染。同时，真空玻璃的热阻很大，真空腔内无空气，也无水汽分子，即使室内外温差达到50℃也不会出现结露现象，令人视野清晰开阔。

　　由于真空玻璃暴露在房屋外面，在使用过程中很容易受到外界环境的腐蚀及不可预料的外力冲击作用，这些都会使真空玻璃的性能退化甚至结构破损，从而失去其节能功能。周期性地对真空玻璃性能进行检测与监测，可以保证真空玻璃的健康状态及其使用寿命，是保证节能建筑发挥节能功效所必须的工作内容。

　　国内外广泛使用的热传导性能测试方法尚无统一的标准，主要使用稳态测量方法。稳态热传导测试方法的基本原理如下：首先被测试的样品两个表面形成恒定的温差，平衡一段时间后，试样内部的温度分布不再随时间变化，即进入稳态热量传递状态，试样内部每一位置通过的热流量相等，最后利用热流量、温差和导热系数之间的关系反解出导热系数。不过，由于真空玻璃热扩散系数很小，为使试样达到稳态热量传递状态，需要较长的实验时间。同时，为了使热流单向一维流动，试验装置必须配备良好的绝热层，同时，样品边界附近的漏热现象将影响到测试结果，而且为了保持被测试的样品两个表面的温差恒定，试验装置需具有良好的恒温系统，从而使得试验装置较复杂和冗杂。

　　文献1 提出在相同热源下，真空玻璃非热源侧温度与传热性能相关，本文在此基础上，提出非稳态传热模型，建立非热源侧温度计算方法并利用CFD 数值仿真技术，进行温度数据分析，并提出在实验中测量温度要注意的事项。

1、真空玻璃

1.1、物理模型

　　真空玻璃通常是由两片玻璃组成，在中间放置微小的支撑物以均匀隔开，在周边采用玻璃焊料熔融封接。然后，通过抽真空后封装抽气孔或者在真空环境下熔封玻璃周边等方法使玻璃之间形成真空层，如图1 所示。

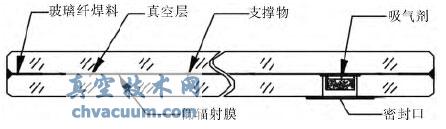
图1 真空玻璃基本结构

1.2、数学模型

　　将真空玻璃在宏观上用均质平板玻璃来代替不连续的支柱排列，应用连续介质假设，将真空玻璃用某一均匀连续介质作为其等价介质，其温度、密度等物理参数都是空间的连续函数，表征其等效的物理性质。

　　当物体的温度随着时间的变化而随之变化时，这个导热过程称之为非稳态导热。导热微分方程及初始条件与边界条件一起，才能完整地描述一个特定的非稳态导热问题。结合傅立叶导热定律与半无穷假设，如图2 所示：将在加热过程中的真空玻璃看作是无限大的，即在时间τ=0 时，位置x=0 处的表面受到扰动，温度t 沿仅且仅沿x 轴方向一维传递。

图2 半无限大物体示意

2、CFD仿真

　　数值仿真技术可以帮助人们完成从最初的基本结构设计到最后的参数优化，利用CFD 软件可以使人们细致入微地观察全部情况。通过数学方程描述物理问题的数值求解的基本思想可概括如下：在时间坐标系与空间坐标系中，原本是连续变化的物理量的场，通过网格划分手段，用数量极多(可以代表物理量的场的特性)但有限个(数学方程可以解出)离散点上的值的来代替原来的物理量的场，这样求解关于这些离散点上的值的代数方程，就可以获得离散点上被求的物理量的值，上述基本步骤可以如图3 来表示：

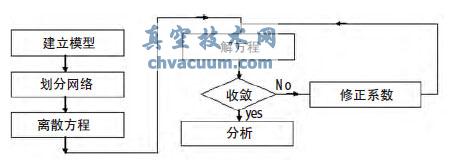
图3 流程框架

　　本文研究内容基于UG、ICEM 和FLUENT 商用软件。运行的计算机主要配置为：处理器：Intel(R)Pentium (R)CPU B950-2.10GHz；内存4GB；操作系统：Windows7 旗舰版。几何模型的准确性和网格划分的质量与数值仿真结果的可靠性息息相关。所以在UG 软件中建立真空玻璃的几何模型时，应尽量与实际情况相一致；用ICEM 软件划分网格后，要注意检查网格质量。在本文中，所有模型都是基于UG8.0版本做出，并导出ANSYS ICEM 可以识别的IGES文件，在ANSYS ICEM 中可以做出质量较高的网格，如图4-1 所示。

　　考虑到在实验过程中，温度是唯一的测量量，真空技术网（http://www.chvacuum.com/）认为它的准确性十分重要。在数学模型中，假设了温度只沿x 轴方向进行一维导热，这样，理论上，只要测得温度与时间的变化关系即可得出导热系数λ 表征的值。不过，在实验中，不得不考虑到温度的y 轴传热过程，即径向传热过程。所以，在实验中就必须合理地解决测温点的选取问题，提高实验的准确性及复现性。

2.1、测温点的选取

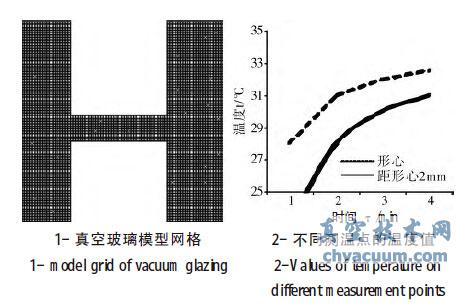
图4 网格划分及温度变化

　　由图4 可以看出，在5 分钟内完全可以测量多个测量点，完成实验。由于支柱和径向热量传输的影响，右侧形心处的温度较其他点温度较高，同时为了避免在实验中出现的随机将测温点布置在温度较高附近，所以，测温点不能仅仅选择一个，而是要在形心某一半径范围内布置多个，取各个温度值，求和作均值化。

2.2、加热片的半径

　　为了构造半无限大条件，降低径向传热的影响，加热片的面积越大越好。如图5 所示，模型厚度10mm，在不同面积加热片时，测温点的温度变化情况。随着加热片面积的增大，也越来越符合半无限大物体的特性，径向导热对测量点的温度影响逐渐变小，相同时刻的温度误差越来越小。当加热片面积增大到一定程度，对精度的贡献及在工程应用上的影响，可以忽略不计。

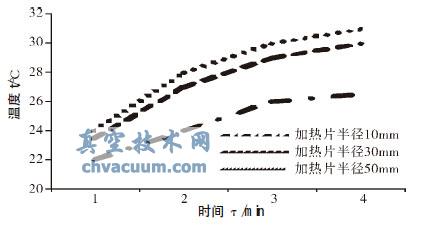
图5 测温点温度与加热片面积关系

3、结论

　　在全球低碳节能浪潮下，真空玻璃将随着产业化进程的加快获得越来越广泛的应用。其相关性能参数的测量也愈发重要。由此，本文建立了非稳态传热模型，得出非加热面的中心温度计算公式，并通过CFD 仿真，分析模型的可行性及指导下一步实验相关测量注意事项。

　　3.1、与稳态测试方法相比，非稳态方法是测量试样升温趋势的动态过程，测试时间长短可以灵活掌控，满足短时间的测试要求。

　　3.2、该方法测量出表征导热系数的同时，也可实现对表征热扩散系数的分析确定。对于评价自身热工性能、分析非稳态过程的研究和应用具有重要意义。

　　3.3、通过建立合理化的传热模型，得到对真空玻璃传热后侧(非热源侧)中心温度实时测量，可以获知真空玻璃的隔热性能优劣和真空玻璃质量的结论。

　　3.4、温度测量是下一步实践中的重点，在测温点及加热片的选取问题中，通过仿真，得出了取多个测量点的测量值，然后求和取均值作为真值；加热片的半径与真空玻璃厚度之比要大于3，具有指导意义。