基于Monte Carlo方法的圆截面直角弯管传输几率

　　借助Matlab软件，用蒙特卡洛方法对圆截面直角弯管在分子流态下的传输几率进行了模拟计算。通过数学方法实现对气体分子的虚拟约束和跟踪。本文先通过模拟最简单的圆直管道传输几率，并与Clausing、Dushman方法进行比较，验证了该方法的正确性和建模的合理性，进而对于圆截面直角弯管的传输几率进行了模拟计算，将模拟结果与两种等效算法比较得出：在分子流下计算圆截面直角弯管的传输几率时，Davis的等效方法较传统的等效方法更为合理。

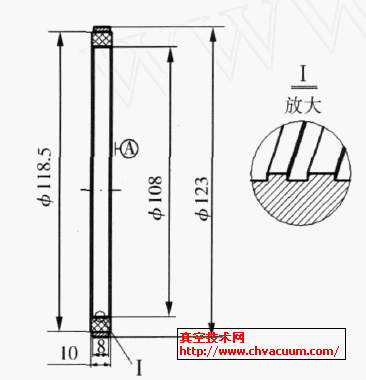
　　在真空系统设计与计算中，为了表征稀薄气体通过真空系统管路元件的流动，通常给出流导几率(即传输几率)，流导几率是确定气体流量的一个重要参数。圆截面直角弯管是真空系统常用的管道结构，其在分子流状态下的传输几率是衡量真空设备和真空性能的重要参数。

1、圆截面直角弯管传输几率的模拟计算

　　1.1、基本假设及概率模型

　　基于管道中的气流状态为分子状态，进行如下假设：

　　(1)气流为稳定气流，气体分子数守恒，即管壁无吸气和放气现象。这意味着射入管口的分子最终只有两种可能：从出口逸出或者从入口逸出。两者的几率之和等于1。

　　(2)入射分子和反射分子都遵循余弦定律。

　　(3)分子在管道内的运动是相互独立的，即分子之间互不碰撞，气体分子只与管壁发生碰撞。

　　(4)评定参数C约等于1，忽略气体分子在分子流态下通过直圆管道的位置束流效应。

　　因为气体以分子流态流动，就每个分子而言，从分子飞入管道与管壁碰撞后产生漫反射直至分子逸出管道，分子的整个运动过程都是随机的。故管道的传输几率本身就是一种概率统计问题。每个分子的随机运动都可以用一个随机变量来表示，通常在计算机上采用(0，1)区间均匀分布的伪随机数进行抽样，用数学方法模拟每个分子的运动过程，根据计算机跟踪每个分子，统计进入管道的分子总数N和逸出管道出口的分子数n，可以得到管道的传输几率Pr

Pr=n/N(1)

　　N越大，Pr越准确。当N足够大时，Pr就足够准确。

　　1.2、圆直管道传输几率

　　在计算圆截面直角弯管的传输几率之前，先进行最简单的圆直管道传输几率计算并与Clausing、Dushman方法计算的传输几率进行对比，验证MonteCarlo法计算传输几率的准确性。圆直管道传输几率的计算方法与圆截面直角弯管的传输几率计算中的横管的部分相似，只不过不用判断分子是否进入纵管，而是直接判断其是否从出口飞出，具体方法在下文中详述。

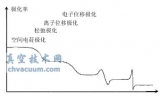
　　利用Matlab软件进行编程模拟，计算出不同长径比的圆直管道的传输几率，将这些数据与Clausing、Dushman方法计算的相应传输几率绘制在同一图中，如图1所示。

图1 MonteCarlo法计算的传输几率Pr和Clausing系数Kc、Dushman的对比

　　从图1中可以看出，用MonteCarlo法模拟计算的传输几率Pr与Clausing积分方程的近似解有很强的一致性。在L/R=1.5处出现最大残差0.0105，造成约1.8%的相对误差。相对误差最大值出现在L/R=17处，达到了5.23%。而Dushman方法计算出来的传输几率与其他两者差别很大，在L/R=5.1处相对误差达到了13.52%。随着L/R逐渐增大，三条曲线逐渐趋于一致。用MonteCarlo法模拟计算的圆直管的传输几率与用Clausing方程计算的近似解十分接近，这证明了该方法模拟计算管道的传输几率的准确性。因此，可以用类似上述的模型对圆截面直角弯管的传输几率进行模拟计算。

2、结论

　　本文主要采用MonteCarlo法模拟计算分子流态下管道的传输几率，先验证MonteCarlo法计算圆直管的传输几率的准确性，再通过与Clausing积分方程的近似解和Dushman近似计算的结果进行对比，得到模拟结果与Clausing积分方程的近似解具有较好的吻合性，Dushman近似计算的结果与MonteCarlo模拟结果相差较大。然后采用该方法模拟计算圆截面直角弯管的传输几率，并与目前常采用的传统的等效长度法、Davis等效法进行对比，传统的等效长度法与模拟结果相差较大，Davis等效法与模拟结果具有较好的吻合性。因此在理论上计算分子流态下的弯管的传输几率时，可以根据Davis等效法来进行计算。