纳米管道中离子分布模型的研究

　　基于纳米管道内离子浓度与电势变化的规律，针对泊松- 玻尔兹曼模型的几种改进方法进行比较说明，并提出使用的限制条件。通过对理论的研究分析，泊松- 玻尔兹曼的分析解很难获得，而仿真的数值解却容易求得，这个结论更有利于进一步的理论研究。

　　随着近代纳米技术的发展，纳流控技术也渐渐走进人民的生活，在医疗检测，信号传输等领域起着越来越重要的作用。在集成芯片方面，纳米尺度的电子元件，二极管三极管的出现等更是电子检测，控制类设备改进的不可或缺的条件。在医疗检测方面，纳米管道可以提高低浓度的离子达到仪器检测标准。在日常资源方面，纳流控技术可以通过纳米管道把海水变成淡水，这个实验已经在实验室成功完成。现在纳流控的技术已经在生活中发挥着重要作用，但是有一些基础的理论却仍然停留在混沌状态，只能通过实验慢慢总结。本篇文章针对纳流控的基础理论模型来进行比较说明，为以后研究打下基础。

1、基础理论

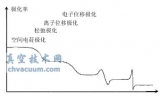
　　通过以前研究我们知道，纳米管道的材料本身具有吸附性，即具有一定的电荷密度，表面电荷密度决定表面电势。同时，管道内溶液又有一定的离子浓度，这样导致管道内离子浓度分布不均匀。溶液阴阳离子分布决定电势分布规律。离子分布可以参考图1。

图1 纳米管道中阴阳离子浓度分布示意图

结论

　　对于经典的泊松- 玻尔兹曼方程，当溶液中阴阳离子的化合价为1:1 时，可以解出具体的方程解。同时，在表面电势值低于25 mV 时，可以用德拜- 胡克公式近似计算，误差很小。当溶液中阴阳离子的化合价绝对值不等时，只能考虑泊松- 玻尔兹曼方程，由于方程没有分析解，一般都转化为PNP 方程来进行模拟，提出的各种算法各有优劣，但是都是模拟计算时候产生的误差而非计算公式的不同。因此很多纳米流的研究人员对不同的PBE 模型与PNP 进行对比，这是没有道理的。同时，在纳流控学科中，管道溶液的速度轮廓由高度大小分布来决定，德拜层是液体流动的动力来源，而水分子之间的内摩擦作用使得溶液流动。纳米级别速度轮廓几乎一致，由于摩擦产生的阻碍速度很小。到微米级别，管道中心速度随尺寸增加，摩擦产生阻碍速度加大，导致流动速度减少，因而速度轮廓形成反向抛物线形状。