承压阀门内漏声学检测方法
分析了承压阀门内漏过程中流体流动状态,以及声源产生机理,建立了阀门泄漏产生的声源信号幅度与内漏率的一般关系. 利用研制的实验台对阀门内漏进行检测实验,并探讨了泄漏时阀门开度、两侧压差等状态变化时的声学特性. 研究结果表明,阀门湍流流场产生的声源主要为四极子声源,其声能随着压差和流速的增大而增强. 因此,可以利用声学方法检测承压阀门是否存在泄漏和估计泄漏率。
0、引言
阀门作为一种通用的机械产品,其安全性一直是人们关注的焦点. 石油、石化是阀门使用率非常高的行业,据统计,购买阀门的费用相当于一个新建工厂投资的8 %. 在用承压阀门中有相当数量的阀门因磨损、腐蚀或其他多种原因往往会出现内外渗漏或泄漏,一般情况内漏很难发现,内漏若不及时发现和处理会导致严重的事故(如输送流体大量流失、串线、起火甚至爆炸,污染环境等) ,因此迫切需要一种实用高效的阀门内漏检测技术. 声学检测具有在线、动态及快速、经济的特点,既可保证阀门的安全使用,又可为维修决策提供依据,降低更换费用 . 因此,声学方法是检测承压阀门内漏的有效方法.
国外从20 世纪60 年代起就开展了阀门泄漏检测技术的研究,目前部分研究成果已经得到了广泛应用. 笔者通过对阀门内漏过程的理论分析和实验研究,确定了阀门内漏率与声学参量的一般关系式,进而可判断阀门是否有内漏,并确定内漏量.
1、阀门内漏产生声源的数学模型
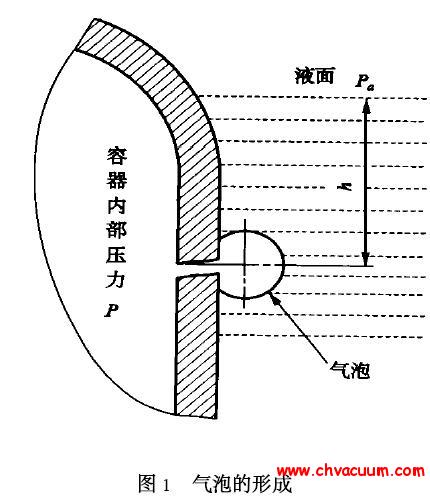
假设内漏模型为充分的泄漏喷射,并分成3 个区域:混合区、过渡区和充分发展区,见图1. 据真空技术网另文介绍:混合区的延伸距离大约是阀门直径D 的4.0~4.5 倍,过渡区距离大致扩展到D 的10 倍. 沿泄漏表面,漏口附近声压较低,在3 至4 倍直径的距离内迅速增加到极大值,以后又慢慢降低,泄漏声音大部分来自混合区和过渡区的湍流运动, 高频噪声主要产生在喷口附近,低频噪声产生在下游,频谱峰在混合区的尖端附近.

图1 阀门内漏分析模型
在喷口稍远的地方为过渡区. 在过渡区中处处充满湍流,平均速度随喷射距离的增加而渐减,射流宽度逐渐扩展. 在喷口更远的地方, 流体成为完全湍流运动, 这就是充分扩展区. 在这个区域里流速逐渐降低以至完全消失,湍流强度变小,产生的声信号为低频性.
阀门内漏时声源产生的基础是流体内湍流产生的波动压力场,流体内漏所激发的应力波为连续信号且具有较宽的频率范围. 湍流是流体流动不稳定的一种情况,在其内部惯性的影响远大于黏性阻力的影响而处于支配地位. 临界流速vc 是该流动条件下层流与紊流的转变流速,它与流体的黏度μ成正比,与流体的密度ρ和管径d 成反比,即雷诺数Rec 由下式表示:
![]()
已经发现当雷诺数在103 到104 之间时湍流开始发生,临界雷诺数稳定在2.0 ×103 左右,其中公认希勒(Schil Ier) 的实验值Rec = 2.3 ×103 ,这种情况可用于估计是否一个给定的泄漏能发生有效的声源.设质量密度为ρ( x , t) ,速度场为v ( x , t) . 假设场中无质量生成(因此, Q = 0) ,质量守恒方程为

微分形式的守恒方程为

利用式(2) , (3) 消去含ρvi 项,可推导出如下的非齐次波动方程

解方程(4) 得

忽略黏滞应力和热应力的影响,则声功率p 为

在没有固体的自由喷流中,马赫数小,声源也小时,声发射的总功率与特征速度的8 次方成正比(所谓四极子声源的特性) . 可是在固体边界效应大的情况下,声源的尺寸比波长小时,发射声的总功率与特征速度的6 次方成正比. 考虑到一般情况,发射声的总功率可表示成与速度的n 次方( n > 1) 成比例. 即在一定的范围内,发射声的总功率随特征速度的增大而增大. 只有四极子声源的情况下湍流噪声功率符合8次方定律: