粗糙度对风力机专用翼型气动性能影响

　　针对风力机专用翼型FFA-W3-211 进行数值模拟，深入系统探讨了粗糙度对该翼型气动性能的影响。采用剪切应力输运k-omega 湍流模型进行CFD 计算; 于翼型表面均匀分布不同粗糙度，求出该翼型敏感粗糙度; 同时，研究了在该翼型吸力面和压力面不同位置布置敏感粗糙度时，粗糙带位置对翼型升力系数和阻力系数的影响，分别求出吸力面和压力面的敏感粗糙带位置，与软件XFOIL 算出转捩点位置进行对比，分析粗糙度对该翼型气动性能的影响。计算结果对风力机专用翼型的设计与开发具有一定的理论价值。

1、前言

　　随着水平轴风力机大型化，由陆地发展到海上，其工作环境愈加恶劣。长期风沙、冰雪、盐雾、动植物等影响，都会引起叶片粗糙度变化，甚至外形尺寸突变。这对风力机的气动性能有较大影响。因此，深入系统地研究表面粗糙度对翼型气动性能的作用机理具有重要工程意义。国内许多学者都对粗糙度进行了相应研究，并得到了一些理论和试验结果: 任年鑫的研究表明，数值模拟方法可有效研究表面粗糙度对风力机二维翼型气动性能的影响; 包能胜等试验表明，在叶片压力面尾缘，通过适当增加一定宽度和粗糙度的粗糙带可增大叶片有效升力系数; 张国强的研究表明翼型前缘和上表面的结冰，对气动性能影响最大。

　　在获取国外学者对FFA-W3-211 翼型试验数据基础上，采用k-omega SST 湍流模型和基于压力的Simple 算法对该翼型进行粗糙度敏感性数值模拟。

2、数值计算模型

　　控制方程采用连续性方程和二维不可压缩雷诺时均Navier-Stokes 方程，分别为：

　　式中ρ———流体密度

　　v———运动粘性系数

　　采用剪切应力输运k-omega ( 即k-omegaSST) 湍流模型。该模型为二方程湍流模型，综合了k-omega 模型和k-epsilon 模型优点，包含转捩和剪切选项，对壁面流固分离有较高计算精度。采用k-omega SST 湍流模型作为数值模拟模型，使结果具有更高的精度和可信度。

3、模型设置

　　3.1、网格拓扑和模拟条件设置

　　FFA-W3-211 翼型是瑞典航空研究院研制的风力机专用翼型，相对厚度为21%，该翼型特点是设计升力系数高，可满足低尖速比风力机要求，最大升力系数对前缘粗糙度不敏感，具有很好的气动性能。广泛用于大型风力机叶片主要功率产生区。

　　拓扑结构采用结构化网格。为研究前缘滞止流动，前缘计算域网格扩展为10 倍翼型弦长; 后缘计算域网格扩展为20 倍翼型弦长，以便研究尾缘附近各种尺度的尾迹涡流动对翼型特性造成的影响。为模拟风洞试验，以更好与试验数据进行对比，几何模型翼型弦长同样取1m。图1 示出该翼型计算域网格拓扑和局部加密。

图1 FFA-W3-211 翼型计算域网格拓扑和局部加密

　　用软件XFOIL 算出该翼型在不同攻角时，吸力面和压力面的转捩点位置，如图10 所示。从图可看出转捩关键攻角为9°，在此攻角下吸力面转捩点在距前缘27%弦长处，压力面转捩点在距前缘54%弦长处。

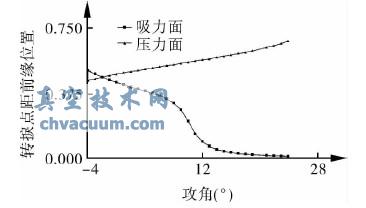
图10 转捩点位置随攻角变化

　　综上可知，FFA-W3-211 翼型处于最佳出力工况时，在粗糙度敏感位置添加一定宽度的粗糙带可适当延缓转捩，但其气动性能与光滑表面时相比大大降低。究其原因为: 增大粗糙度后流场扰动加剧，层流向湍流过渡段区域增大，故推迟了转捩点位置; 而流场扰动的加剧迫使该翼型气动性能急剧恶化。文献中所提在叶片压力面尾缘，适当增加一定宽度和粗糙度的粗糙带可增大叶片有效升力系数的结果并不适用于该翼型。

5、结论

　　( 1) 数值模拟采用k-omega SST 湍流模型，可有效研究表面粗糙度对FFA-W3-211 翼型气动性能的影响;

　　( 2) 与工程实际运行时间相联系，模拟了FFA-W3-211 翼型表面粗糙度对其升力系数和阻力系数的影响，通过分析，总结出该翼型的敏感粗糙度为0. 6mm;

　　( 3) FFA-W3-211 翼型敏感粗糙带位置为: 吸力面距前缘55%弦长处和距前缘90%弦长处; 压力面距前缘45%弦长处和距前缘90%弦长处;

　　( 4) 在FFA-W3-211 翼型敏感粗糙带位置布置0. 6mm 粗糙度可推迟其转捩点，但并不能改善其气动性能。在翼型压力面尾缘增加适当粗糙度的粗糙带可增大翼型升力系数的结论并不适用于该翼型。