风冷无油涡旋空气压缩机涡盘温度场数值计算

　　涡盘温度场是变形计算的基础，为了进行温度场的有限元计算，通过压缩区域的划分，把动态的空气压缩过程转换为静态的热通量边界条件，由冷却风测量结果计算得到冷却风换热系数边界条件。假设涡齿温度在展角整个范围线性分布，动、定盘涡齿平均温差为0℃，对涡盘温度场进行了初次计算，在温度场初次计算结果与定盘温度测量值对比以及涡齿几何特点分析的基础上，以涡齿温度线性起始角、动、定盘压缩区域平均温差为调整参数，热通量计算时的动、定盘涡齿温度条件和有限元温度场计算结果误差介于±0. 2℃为目标，进行热通量和温度场的迭代计算，得到了与热通量计算时涡齿温度条件、定盘温度测量结果相符的涡盘温度场。

　　涡旋压缩机有稳定、高效、可靠的优点，其切向泄露完全取决于动定涡盘径向间隙，径向间隙过大，排气量、排气压力、效率下降，径向间隙过小，工作过程中涡盘温升变形，容易导致碰撞，不能正常运行。空气的比热容较小，风冷无油涡旋空气压缩机工作过程中温度较高，温升对涡盘变形的影响更为明显，为了获得涡盘温度升高后的变形规律，确定合理的配合间隙，以及对涡齿进行局部修正，首先需要求解涡盘温度场。

　　有限元计算常用于温度场、变形的求解，计算结果的准确与否，与边界条件紧密相关。已有的涡盘温度场研究缺乏实验验证，研究过程涡盘简化为涡齿，涡齿温度按照展角直接线性加载，或分块加载测量点的温度，或按照涡盘半径线性加载，或涡盘中心位置加载排气温度，边缘位置加载吸气温度，由于容腔位置在不断变换，且内外容腔移动速度并不相同，无法确定换热系数的准确值和有效控制换热系数加载位置的移动，在压缩区域以换热系数的方式加载边界条件也并不合适，这些温度场计算模型均与实际出入较大。而使用流固耦合计算时，流场网格需要进行重构，径向间隙处网格质量不能满足计算要求。

　　本文把动、定盘压缩区域划分为多个子区域，由空气压缩的热力学过程计算得到各子区域的热通量，作为温度场计算压缩区域的边界条件。热通量计算时若子区域内涡齿的温度较高，则该子区域的吸热量较少，热通量计算结果较低，导致温度场计算结果低于热通量计算时的涡齿温度，相反温度场计算结果则高于热通量计算时的温度，基于这过程，首先预设热通量计算时压缩区域的温度边界，与温度场计算结果进行比对后，调整热通量计算的温度边界，直至两者相符，从而得到与热通量计算时温度边界、定盘温度测量值一致的动、定盘温度场。

　　1、定盘温度测量及换热实验关联式

　　1.1、定盘温度测量过程

　　空气涡旋压缩机测试平台由合肥通用机械研究院研制，通过了国家标准验收。测试平台主要包括PC 机、电机、PK69 型启动控制柜、JK69 型仪表柜、热电偶、MDM3051 智能压力/差压变送器、储气罐。从涡齿外端，每π 个展角钻一个深入涡齿的测温孔，用Pt100 热电阻测量定盘涡齿温度分布，如图1所示。

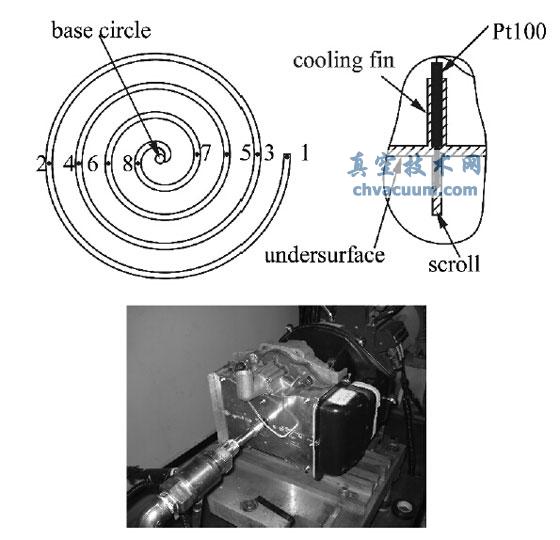
图1 涡齿温度测量

　　1.2、格林尼斯基换热实验关联式

　　冷却风和压缩空气均为强制对流换热，格林尼斯基公式是常用的对流换热实验关联式，既适用于过渡流也适用于湍流，已包含了短管入口修正

　　式中，Nu 为努塞尔数，Re 为雷诺数，Pr 为普兰特数，fg为达尔西阻力系数，费罗年柯公式表达为：fg =(1.82lgRe -1.64) ^-2，Dequal为管道当量直径，Dcurve为管道的弯曲直径，l 为管道长度，空气压缩过程时取内涡旋线长度，Tg为空气温度( 单位为K) ，Tw为壁面温度( 单位为K，在温度场计算过程中动态提取换热面平均温度) 。

　　2、结论

　　通过对冷却风风速和冷却风排气温度的测量，计算出动、定盘冷却风质量流量，结合动、定盘冷却风流道尺寸测量结果，由格林尼斯基对流换热系数公式得到了冷却风换热系数，并对定盘换热系数进行了弯曲管道效应修正，对动盘冷却风换热系数进行了振动效应修正。

　　通过子区域的划分，结合气体压缩过程热力学过程，得到了子区域各换热面积的热通量，为动、定盘温度场计算边界条件的设定提供了一种可靠的方法。

　　通过热通量计算时涡齿温度的设定值和温度场计算结果的对比，对涡齿温度线性分布起始角和动、定盘压缩区域平均温差进行调整，迭代得到了与热通量计算时涡齿温度设定值、定盘温度测量值一致的动、定盘温度场。

　　动、定盘涡齿温度场等温线呈螺旋状向外展开，散热区域温度场等温线分布接近于漏斗状，温度场的分布特点与风冷涡旋空气压缩机压缩、散热过程相符。