泵用不可压缩流体密封刚度系数分析

2014-08-17 张盟大连理工大学能源与动力学院

　　针对不可压缩流体密封弹性支承的问题，分析了负刚度产生的原因。选用三维流动模型，数值求解Navier-Stokes 方程。采用k-ε 湍流模型，计算LNG 泵的节流衬套和口环密封的动力特性系数，分析在LNG 泵不同转速工况下，不可压缩流体密封的动特性变化，并与2 倍间隙密封的动特性相比较。模拟了密封腔内部流场，通过分析比较密封圆周上压力和速度分布，研究等截面环形产生负直接刚度的原因和影响因素。研究结果表明：等截面环形密封和槽道式密封的1 倍间隙直接刚度小于2 倍间隙，1 倍间隙交叉刚度大于2 倍间隙，密封磨损后稳定性反而提高;转速升高使等截面环形密封和槽道式密封的直接刚度下降，交叉刚度增大，造成稳定性下降;等截面环形小间隙密封，在高转速工况下容易产生负直接刚度，影响转子的稳定性，工程上建议采用槽道式密封控制不可压缩流体泄漏。

　　泵叶轮入口轮盖与进口导流管间存在动静间隙。部分高压流体经叶轮出口间隙外泄，并重新回流至泵入口，这股回流既消耗主泵的功率，也干扰主流场流动，同时减小有效通流面积，降低泵的流动效率和性能。为了尽量降低这种泄漏，在动静间隙上设置非接触式不可压缩流体密封。

　　非接触式密封技术广泛应用在泵等旋转机械中，它能够有效控制旋转部件与静止部件间的泄漏。对于转子动力系统，密封会提供附加的刚度和阻尼，这对转子的稳定性造成一定的影响。Childs 等对控制体方法不断改进。Arghir 等发展了CFD 方法，并计算动力特性系数。Benckert 等做了大量的关于动力特性的实验，并证明密封的交叉刚度是由密封周向流动引起的，他们在实验中测量了不同类型密封的直接刚度，发现较长密封的直接刚度为负值。Leong 等[9]蒸汽轮机迷宫密封做了大量试验，结果与Benckert 等的测量结果很吻合，多数密封直接刚度为负，少量短密封为正。Mihai 等[10]发现进出口压差较小时，出口有回堵现象，动力特性系数中的直接刚度系数出现负值，影响转子的对中效应，转子稳定性差。国内何立东等用实验和数值方法研究动力特性系数。模拟仿真方面，孙婷梅等利用CFD有限元软件Fluent 计算迷宫密封三维流场，研究了偏心率、入口预旋、涡动速度对密封动力特性的影响，密封直接刚度维持在负值范围，他们计算出密封周向压力分布曲线，但是没有分析产生负直接刚度的原因。

　　本文应用数值模拟结合工程实际，利用CFD 有限元软件Fluent 计算LNG 泵的节流衬套和口环密封的动力特性系数，模拟在LNG 泵不同转速工况下，不可压缩流体密封的动特性变化，通过分析比较密封圆周上压力和速度分布，研究等截面环形密封产生负直接刚度的原因和影响因素。

密封模型

涡动转子数学模型

　　本文假设整体计算域为湍流，湍流模型采用标准的k-ε 模型，近壁面采用标准壁面函数：

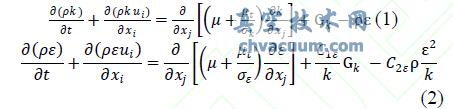
泵用不可压缩流体密封刚度系数分析

　　式中：k G 表示由平均速度梯度产生的湍动能项，b G表示由浮力产生的湍动能项，M Y 表示由可压缩湍流中，耗散率的波动项，方程常数项中C1 =1.44 ，2 C 1.92   ，C = 0.09 ，还有=1.0 k  ， =1.3   分别是湍动能k 和湍动能耗散率ε 的湍流普朗特数，k S 和S 是自定义源项，标准k-ε 湍流模型是半经验公式。

涡动转子动力学模型

　　本文采用旋转坐标系，在转子中心定义坐标系，转子与静子的相对位置不变，坐标系变换把非定常问题转换成定常问题。图1 所示偏心转子在静子中涡动受力，e 为转子偏心距，本文假设转子绕静子中心以圆形轨迹涡动，涡动半径是转子偏心距e，涡动角速度是Ω ，转子的旋转角速度是ω ，转子的旋转角速度与涡动角速度比值定义为涡动比。涡动轨迹的径向力和切向力Fr、Ft。

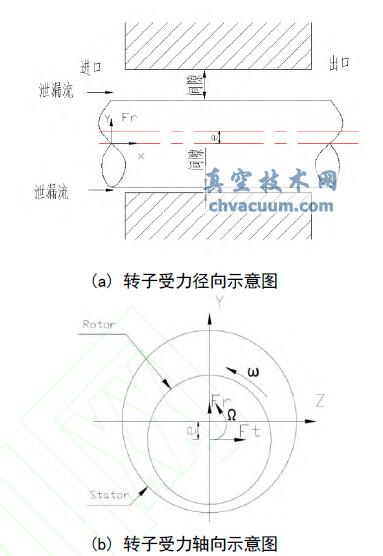
偏心转子在静子中涡动受力示意图