机械密封端面磨损率的一种简易计算方法

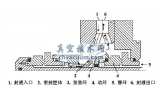
　　机械密封端面材料通常采用软─硬组对形式，硬质环端面比软质环端面光滑得多，且变形及磨损极小，可以简化为刚性理想光滑平面。对于设计和使用合理的机械密封，其软质端面的磨损形式主要表现为黏着磨损。工作时，机械密封端面间的接触发生在软质环端面较高的微凸体上。摩擦时接触点处发生变形而产生黏着，随后在滑动中黏着结点被摩擦力剪切破坏。这种黏着、破坏、再黏着的交替过程就构成黏着磨损。用来计算黏着磨损的方法很多，但大多都建立在Archard 磨损理论模型之上。Archard 于1953 年，在假设接触的两表面是由许多高度相等、半径为r 的半球形微凸体组成的条件下，提出了黏着磨损的计算方法。图1 是黏着结点的形成与破坏示意图，图中Fc为端面比压，v 为端面平均线速度。

(a) 黏着结点形成 (b) 黏着结点破坏

图1机械密封黏着结点的形成与破坏

　　顾永泉基于Archard 磨损理论给出了机械密封端面磨损率的一种简易计算方法，其表达式为:

　　式中γ———机械密封端面磨损率，m

　　K_w———磨损系数，表示黏着结点产生磨屑的概率，与摩擦副材料和工作条件有关

　　H₂———软质环材料的布氏硬度，Pa

　　p_c———密封端面比压，Pa

　　v———密封端面平均线速度，m/s，v = πrmn /30

　　rm———密封端面平均半径，m

　　n ———转速，r /min

　　式(1) 中的磨损系数Kw是一相似准数，为一概率系数，例如Kw = 10 ^-6 即表面接触点的每1000000 次接触会产生一次磨损，它集中反应摩擦副端面的摩擦状态、滑动速度、温度、界面反应及材料性能的综合影响，是摩擦学系统的函数。磨损系数Kw值越小，磨损越少，常由磨损试验测算。真空技术网(http://www.chvacuum.com/)查阅到部分机械密封摩擦副材料的磨损系数Kw值值得注意的是，式(1) 是由Archard 黏着磨损理论模型得出的，它在某种程度上描述了机械密封端面磨损的一般规律，但是Archard 理论中假设微凸体是半径均相同的半球体且没有考虑摩擦力的影响，因此，这个磨损公式本身与工程实际有一定差距。