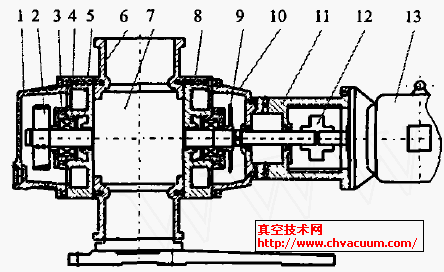
密封环端面共聚焦扫描图像的分形特征研究

2015-10-16 张浩南京林业大学机械电子工程学院

　　基于分形理论，利用MATLAB 开发密封环端面激光共聚焦扫描图像分形维数计算及分析程序，利用Sierpinski地毯对程序的计算结果进行标定，计算不同分割阈值下的图像分形维数，给出一种分割阈值的选取方法。研究结果表明: 设计开发的分形维数计算程序具有较高的准确性; 图像分割阈值的选取对密封环端面分形维数的计算有重要影响，给出的分割阈值选取方法，能使图像二值化效果最佳，使扫描图像能最大程度地反映密封环端面形貌的分形特征，从而提高密封环端面形貌定量描述的精确度。

　　密封环端面的形貌是机械密封加工和工作过程中表现出来的重要特征，它对机械密封的摩擦特性和密封特性具有重要影响。研究密封环摩擦副粗糙表面的固有特性，正确表征摩擦副的表面形貌，对了解密封端面间的泄漏通道状况，以及提高机械密封动静环接触端面的磨合质量具有重要的意义。

　　20 世纪70 年代，法国数学家Mandelbrot正式提出并创立了一种探索自然界复杂形态的数学分支———分形几何学。分形几何能够在更深层次上深刻地描述、研究和分析普遍存在的杂乱无章的、不规则的、随机的自然现象，在摩擦磨损领域中引入分形理论实现了对摩擦副粗糙表面形貌的科学的定量描述，从而推动了机械密封端面形貌与探寻密封泄漏通道的研究。在一些基于分形理论的机械密封端面研究中，大多采用W-M 或M-B 函数来表征和模拟密封端面，同时利用功率谱法和结构函数法来研究轮廓曲线的分形特性，但是函数模拟只能得到统计意义上的形貌，并不能全部反映密封端面的泄漏通道情况，因此利用扫描图像来研究密封端面的形貌特征就具有重要的意义。在以往一些基于扫描图像的分形特征研究中，多结合图像处理技术对图像进行预处理，然后利用计盒维数等方式求取二值化后图像的分形维数，然而二值化过程中阈值的选取对图像的特征表现和分形维数计算具有重要的影响，所选取的分割阈值应能最大程度地将密封端面扫描图像的分形特征表现出来。

　　本文作者拟利用密封环端面的激光共聚焦扫描图像，通过MATLAB 编程计算密封端面的分形维数，讨论二值化过程中分割阈值选取对分形维数的影响，给出一种图像分割阈值的选取方法，突出图像的自相似特征，从而为密封环端面的分形表征提供一种快速、精确的新方法。

　　1、基于MATLAB 的分形维数算法设计

　　分形维数是分形几何理论中最重要的基本概念之一，目前已经有很多维数的定义，主要包括Hausdorff维数、计盒维数(CBD) 、修正计盒维数、填充维数等。Hausdorff 维数是分形几何理论的基础，可以说分形几何的理论体系是建立在这一基础之上，但是Hausdorff 维数只适合分形几何的理论推导，只能通过分析的方法获得一小类规则的纯数学分形的Hausdorff维数，它对实际应用中提出的分形维数的计算问题无能为力。鉴于此，人们提出了计盒维数的概念，由于计盒维数物理含义直观，易于进行程序化计算，因此得到了广泛的应用。

　　1.1、计盒维数的原理

　　设A 是Rn 空间的任意非空有界子集，对于任意一个r>0，Nr(A) 表示用来覆盖A 所需边长为r 的n维盒子的最小数目。如果存在一个数DB，使得当r→0 时，有

密封环端面共聚焦扫描图像的分形特征研究

　　计盒维数这个形式的定义在实际中有广泛的应用。在计算一个平面集A 的计盒维数时，可以构造一系列边长为r 的正方形，然后计算不同r 值的盒子与A 相交的个数Nr(A) ，这个维数是当r→0 时，Nr(A) 增加的对数速率，或者可以由函数lnNr( A) 相对于lnr 图的斜率的负值来估计。

　　1.2、程序设计

　　图像在计算机中是以矩阵的形式存储，一幅长度为M 个像素，宽度为N 个像素的图像，可以看成是一个M×N 的矩阵，矩阵的每一个元素代表一个像素，元素的值是像素点颜色或索引色。利用激光共聚焦获得的密封环端面图像是RGB 格式，无法直接进行计盒维数的计算，因此需要对图像进行预处理，包括灰度变换、平滑滤波、降噪等，再选取一个合适的分割阈值，将图像二值化，这样就将图像处理成只包含0 (孔隙) 和1(固体骨架) 的二值矩阵。根据计盒维数的原理，可以通过MATLAB 编写程序计算计盒维数，步骤如下：

　　(1) 读取二值化的密封环端面图像，并将其数值矩阵赋值给变量H；

　　(2) 用不同边长尺寸的正方形盒子对矩阵H 进行覆盖，统计在不同尺寸r 下包含目标像素(0—孔隙) 的盒子数，计入数组Nr中；

　　(3) 在双对数坐标中利用最小二乘法对(lnr，lnNr) 进行拟合，得到直线斜率的负数即为图像的计盒维数。

　　程序的流程图如图1 所示。

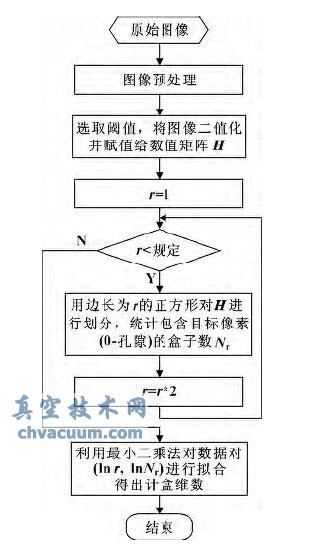
密封环端面共聚焦扫描图像的分形特征研究