真空泵爪形转子的平衡方法研究
用去除材料的方法对爪式转子做平衡分析,利用平衡理论计算得出待移除的质量m 和待移除质量m 在转子上的分布位置A(x, y, z)。然后借助Pro/Engineer、Adams 等仿真工具对去除质量后的转子进行平衡的模拟仿真,得到模拟的平衡结果。传统的平衡方法是将转子放到平衡机上,用试探性的方法去除材料,然后来验证平衡效果,这样要反复实验才能得到满意的结果。将仿真结果和直接在平衡机上做的平衡效果进行比较,结果表明:前者平衡效果比后者好,从实际的操作角度来说,前者一步到位,不用反复试验,节省时间。
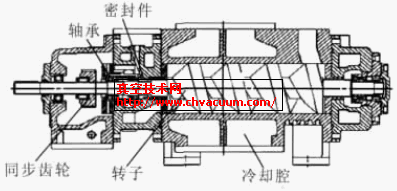
爪式转子无油真空泵,是一种性能优良的干式真空泵,它可代替传统的油封机械泵。现已在石油、化工、制药、食品加工、电子、半导体、航空航天、核工业等领域得到广泛应用。而爪式转子,作为无油干式真空泵的核心部件,其各个方面的精度直接影响着干式真空泵的工作效率和工作的稳定性。这其中最为关键的技术之一就是爪形转子的如何平衡问题。做好转子的平衡,可以减轻工作时轴对轴承的压力,从而增加轴承寿命。减轻传动齿轮之间的相互摩擦,增加工作效率。
1、平衡理论分析
1.1、转子不平衡的原因分析
由于设计、结构、材质不均匀、形状不规则及制造安装误差等原因,所有实际转子的中心惯性主轴都会偏离其旋转轴线,这样,当转子转动时,转子各微元惯性力所组成的力系不是一个平衡力系,这就是我们常说的转子的不平衡。设有一爪形转子,质量为m,以等角度ω 绕一固定轴旋转,取其转轴上任意一点o 作为坐标原点,转轴为z 轴,并作出相应的ox 及oy 轴,转子质心坐标为C(xc,yc,zc),质心C 对旋转轴z 的矢径为rc,转子中任意质点坐标为mi ( xi,yi,zi)对转轴的矢径为ri,则由理论力学知识可知,该惯性力系向坐标原点o 简化,可以得到一主矢Ro和主矩Mo。主矢和主矩的计算公式为:
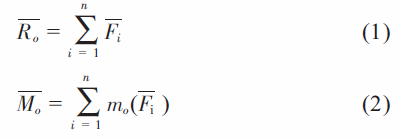
式中,Fi 为质点mi 产生的离心力, 大小为miriω2,其指向离心方向,为矢径ri 的方向,故
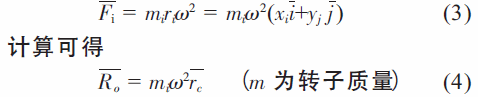
简化的主矢Ro 的大小与方向和转子质心的离心惯性力相等,只不过作用于o 点即Ro//rc,其大小与方向和简化中心o 点的位置无关而惯性力系向o 点简化的主矩可写为
![]()
式中,Mx,My 及Mz 为主矩Mo 在坐标轴上的投影,其大小等于力系所有各力对该轴之矩的代数和,它们都和o 点的位置无关。
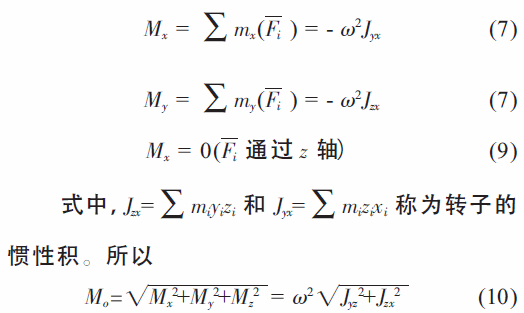
由以上分析可知,转子的惯性力向任一点简化的结果一般得到一个力和一个力矩。转子在旋转时,主矢和主矩方向都在变化,其矢量随同转子一同旋转成为引起轴承振动的激发源。所以,转子平衡的充分必要条件就是:惯性力系向任一点简化的主矢和主矩都为零,即
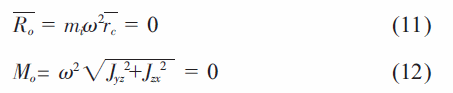
由Ro= 0,则rc= 0,这说明旋转轴必定通过质心C;由Mo=0,则Jyz+Jzx=0,满足条件的转轴z 成为惯性主轴,通过质心的惯性主轴成为中心惯性主轴。因此,要消除转子对轴承的动压力只需旋转轴是中心惯性主轴。由于爪形转子形状不规则,因此其对旋转轴为中心的质量分布不对称。所以,爪形转子大都是不平衡的。要使一个不平衡的爪形转子变为平衡转子,就要重新调整转子的质量分布,即在其某个部位加重或者去重,使转子的中心惯性主轴和旋转轴一致。这时,其惯性力系能够满足(11)和(12)式,转子成为平衡转子。
1.2、质量代换的质量划分方法
爪型转子的理论型线为ABCDEFGHA 组成的轮廓,由6 段曲线组成。
第1 段:曲线AB 与另一转子上的对应点F共轭,为一段摆线。
第2 段:曲线BC 与另一转子上的对应圆弧EF 共轭,为一段圆弧。
第3 段:曲线CDE 与另一转子上的对应点E共轭,为一段摆线。
第4 段:曲线EF 与另一转子上的对应圆弧BC 共轭,为一段圆弧。
第5 段:曲线FG 与另一转子上的对应点A共轭,为一段摆线。
第6 段:曲线AHG 与另一转子上的对应圆弧AHG 作纯滚动。
具体的转子型线轮廓,如图1 所示。
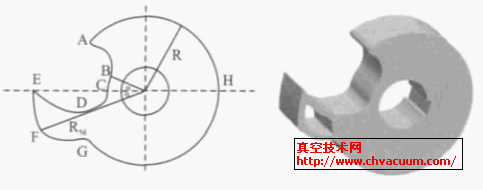
图1 爪形转子的理论型线 图2 面积拆分示意图
从上面的分析我们可以知道,转子型线并非规则的对称图形,所以质心并不在其旋转轴心,从而不能正常工作,我们需要将转子部分质量移除,以达到平衡的目的。移除质量时我们用到了质量代换法这种方法就是将构件用若干集中质量来代换,使这些代换质量与原质量在动力学上等效。具体的代换条件有如下,
(1)代替前后构件的质量不变
![]()
(2)代替前后构件的质心位置不变

(3)代替前后构件对质心轴的转动惯量不变
![]()
注:其中构件质量、质心位置、对质心转动惯量分别为m、s、Js。