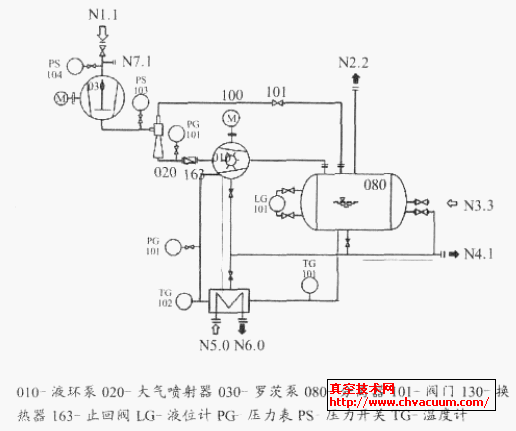
罗茨转子取得最大形状系数的通用判据研究

　　为研究罗茨泵用转子取得最大形状系数的几何特征，在定义转子主型线段的基础上，采用共轭几何上的欧拉-萨伐里方程法，由谷主型线段的曲率半径为0 的极限点，倒推出峰主型线段上共轭的最大形状系数点，据此确定出峰主型线定义中的待定系数，并进而给出转子最大形状系数的计算方法。结果表明，转子取得最大形状系数等价于最大形状系数点、曲率中心、转子中心构成一以曲率中心为直角点的直角三角形的通用判据1，和最大形状系数点处的曲率半径被其瞬心所平分的通用判据2; 转子取得最大形状系数与通用判据间互为充分必要条件，且仅能确定出峰主型线定义中的2 个待定系数。

　　罗茨泵是一种依靠一对同参数转子副的转动，从而实现工作腔容积周期性变化的流体机械，应用广泛，这对转子称为罗茨转子，其型线质量直接影响泵的性能。目前可采用的主要有圆弧型、渐开线型、摆线型、直线型或彼此组合型；研究内容上主要有型线理论、型线设计、型线创新等。

　　转子的最大形状系数是罗茨泵一个重要参量，与谷部强度、啮合密封长度等参量共同形成了泵的特性。其中，形状系数是影响泵容积利用系数或容积效率的决定性因素; 形状系数越大，容积利用系数或容积效率越高，谷部强度虽有削弱但可通过优选材料来加以弥补，因此泵设计尤其是轻量化设计的重点在于形状系数的最大化。

　　目前，通过转子共轭关系、极限几何等方法，虽然给出了2、3、4 叶圆弧转子的1. 67、1. 48、1. 37，渐开线转子的1. 62、1. 46、1. 37 的最大形状系数。但这一针对具体型线的特定方法，所涉理论相对深奥，既不利于工程技术人员的直接采用，也不利于创新转子的最大形状系数预测。为此，旨在通过泵用转子取得最大形状系数的通用判据及计算方法的提出，以期实现转子最大形状系数快速、高效、准确的计算与评估。

1、 主型线段的定义

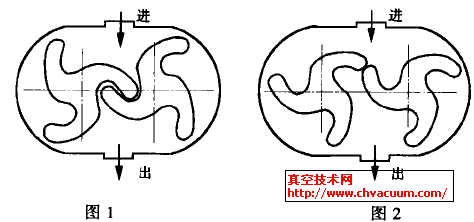
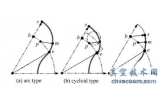
　　无论是转子的实际型线还是理论型线，均由节圆之内的谷部型线( 简称为谷型线) 和之外的峰部型线( 简称为峰型线) 组成，如图1所示。

图1 三种不同的型线类型

　　其中，峰型线可由单一型线段构成，如图1(a) 、(b) 所示的单一圆弧、单一摆线; 也可有多型线段构成，如图1(c) 所示的过渡用顶圆弧段、共轭用渐开线段的双型线段，其中，过渡用顶圆弧段的几何尺寸完全由共轭用渐开线段所唯一确定。

　　定义转子叶峰部的、谷部的对称轴分别为峰轴、谷轴；型线段中端点位于节圆上的为主型线段，其中，峰部的为峰主型线段，谷部的为谷主型线段。由于峰主型线段上的任一点m在由起点s向终点e的共轭移动中，m点处的法线与节圆的交点p( 即为对应于点m 的瞬心) 也从峰轴与节圆的交点b 向终点e 逐步移动，因此，峰主型线段和谷主型线段共同构成了转子的本体共轭运动。

2、主型线段间的极限共轭条件

　　以主转子的轮心o1为原点，峰轴为y 轴，构建xo1y 直角坐标系，如图2所示。取峰主型线段上的任一点m，记o1p 连线与y 轴间的夹角为θ；y = f(x)为峰主型线段函数，其具体形式由选定的峰主类型(比如圆弧型、渐开线型等) 及其函数表达式中对应的待定系数所唯一确定。

6、结论

　　(1) 转子取得最大形状系数等价于谷主型线段上存在最小曲率半径点，峰主型线段上存在最大形状系数点，其中，最小曲率半径点和最大形状系数点互为共轭关系。

　　(2) 转子取得最大形状系数的通用判据为最大形状系数点、曲率中心、转子中心构成一以曲率中心为直角点的直角三角形，以及最大形状系数点处的曲率半径被其瞬心所平分。

　　(3) 转子取得最大形状系数与通用判据间互为充分必要条件，且仅能确定出主型线段中的2 个待定系数。