磁悬浮分子泵的振动抑制

　　2000 L 磁悬浮分子泵研制中，遇到复杂振动问题：转子弯曲模态共振; 陀螺效应造成动力学失稳; 叶轮叶片导致转子颤振; 成因复杂的机电耦合模态振动。它们同时出现，严重影响转子稳定性，给振动抑制带来困难，需进行精细的控制器设计。控制器中，对不同振动采用不同方法抑制：陀螺效应依靠交叉反馈控制; 弯曲共振、分子泵叶轮叶片颤振及机电耦合模态振动，依靠各种不同的控制器传递函数相位整形方法。试验验证了方法的有效性，分子泵平稳升速到24000 r/ min，样机达到了设计真空性能指标。

　　涡轮分子泵是获取高真空的一个重要设备，被广泛应用于高真空场合。相较于传统滚珠及油膜轴承，电磁轴承作为一种新型轴承，因其非接触、无摩擦、低功耗、维护成本低、动力学可控并可对转子动不平衡进行主动控制等特殊优点，在工业应用上前景广阔。对真空设备而言，非接触悬浮是很有吸引力的。电磁轴承应用于涡轮分子泵，可实现分子泵的无油、无磨损运行，运行安静，振动极小，尤其适合半导体工业等超净高真空应用场合。在此，将介绍2000 L 五自由度磁轴承涡轮分子泵样机研究进展，重点关注磁悬浮分子泵试验研究中遇到的各种复杂振动抑制问题。这些振动问题由各种因素所导致，包括泵转子的弯曲模态振动，陀螺效应造成的转子动力学失稳，泵叶轮上叶片的颤振及一个由转子与分子泵永磁电机共同导致的复杂振动模态。这些因素同时出现，并且均能对泵转子的稳定性造成破坏，必须在磁轴承控制器设计中同时解决，给控制器的设计带来大的困难。

　　在分子泵转子设计中，转子一阶弯曲模态频率已经尽量保持远离转子最大工作转动频率即400 Hz,但其对转子振动的影响依然不能忽略，尤其在高速运行时，陀螺效应造成一阶弯曲振动反向涡动模态频率下降明显。通常认为传统轴承支承的转子，反向涡动很难被激发，但对电磁轴承转子系统，经常可观察到反向涡动被激发出来。因此，在转子工作于整个转速范围内时，均应为弯曲模态振动提供足够阻尼，避免一阶弯曲正向或反向涡动被激发。事实上，如果电磁轴承振动控制不考虑弯曲模态的阻尼,转子静态悬浮时就会把转子弯曲振动激发出来。

　　由于分子泵转子芯轴上安装有抽气涡轮，其惯量比，即转子极转动惯量与赤道转动惯量之比，较大，转子陀螺效应明显，陀螺力矩会对磁轴承转子模态的稳定性造成大的影响。除上边所提到的对弯曲模态的影响，陀螺效应对转子刚性模态的影响更加显著。如果控制器中没有采取相应的措施，当转子远未到达其最大工作转速时，转子章动( 转子前向涡动刚体模态) 和进动( 转子反向涡动刚体模态) 就会被激发，破坏转子稳定性。泵叶轮上的叶片，因其厚度不大，刚度偏低，单片叶片动力学模型类似悬臂梁，其一阶弯曲频率主要落在中频段，即主要落在300~ 400 Hz 之间。转子要到达其工作转速，必须穿越这些模态频率。如果没有适当的应对措施，当转子同步频率接近某个叶片模态频率，对应的叶片模态振动会被转子不平衡振动所激发。

　　在各种振动问题中，转子与泵永磁电机的动力学耦合导致的振动模态是最令人困惑的，也是最难解决的。此振动模态在220 Hz 附近有固定的振动频率，对其机理难以给出清晰解释，但它确实与永磁电机状态相关。在前期安装了交流异步电机的测试泵上，没有观察到这样的振动模态。在转子静态悬浮及电机低速运行时，该模态振动很难观察到，而一旦转速升到一定范围，尤其当转子章动频率接近该模态的特征频率，该模态会变得很危险，其稳定性减小，最终会破坏转子的动力学稳定。

　　为同时应对出现的这些振动问题，在控制器中使用了不同的针对性方法。陀螺效应导致的失稳通过交叉反馈方法解决。弯曲模态、叶片颤振、220 Hz耦合模态等其它振动问题，均通过相位整形控制方法解决，但对应不同的问题，应用了不同的相位整形措施。

　　在文中，给出了这些振动抑制相关的试验结果,转子最终能稳定运行于其最大工作转速24000r/ min。最后，给出了磁悬浮分子泵样机所达到的基本真空性能指标。

1、分子泵转子系统

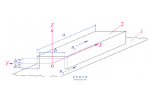
　　涡轮分子泵结构如图1，其中( x1，y1) 为上径向磁轴承中心平面坐标，( x2，y2) 为下径向磁轴承中心平面坐标。

图1 分子泵结构及磁轴承坐标

　　分子泵转子的钢质芯轴上热装了永磁电机转子，头部用5 个螺栓安装上一铝合金叶轮。分子泵转子部分参数见表1。

表1 磁悬浮分子泵参数

　　分子泵转子上有复杂的动力学特征，包括叶轮叶片模态、转子弯曲模态及转子上明显的陀螺效应。就转子结构设计而言，为了避免超越弯曲临界运行,即保证转子运行于次临界状态，降低磁轴承承载及振动控制的难度，转子设计必须保证：在整个工作转速范围内，转子一阶弯曲频率远离转子工作频率，即转子工作于次临界状态。

　　其动力学特性可通过有限元(FEM) 方法计算。

　　由于叶轮上叶片众多，为简化计算分析过程，将叶片模态分析与转子整体模态分析分开进行。在进行叶片模态分析时，把叶轮上各层叶片均简化为固结于无限大基础上的悬臂梁，分别进行模态分析，所得频率分别约为330，370 及730 Hz。在对转子进行整体建模时，把叶轮换为一个无叶片的模拟轮，此模拟轮与真实叶轮有相同的重心位置及转动惯量参数。在安装了模拟轮的转子上，可分析分子泵转子的整体动力学模态。

　　简化后的转子模型，与真实转子具有基本相同的动力学特性，可用于转子结构评估及磁轴承控制器设计等工作。在进行转子动力学分析时，根据简化模型的轴对称性，模型进一步简化为二维模型，即2D 傅里叶多谐波单元构建的轴对称模型。2D 傅里叶多谐波单元，可以准确地描述结构的轴向变形、扭转变形和弯曲变形。对剖面形状复杂，且陀螺效应明显的转子系统，利用该单元可以进行高效的转子动力学有限元分析。转子2D 模型见图2。图中,转子的上下径向磁轴承中心处，均由刚度为500 N/ mm的弹簧单元支承。

图2 转子2D有限元模型

　　经有限元计算分析，转子前两阶弯曲模态频率分别为538 及1730 Hz。可知，静态下转子最大工作频率400Hz 远小于转子一阶弯曲频率，但由于转子存在明显陀螺效应，必须考虑其对模态频率的影响。转子坎贝尔( Campbell) 图如图3 所示。从图中可以看到，转子的刚性模态频率与弯曲模态频率受到转子陀螺效应的影响均非常明显。当转子转速升高,转子进动( 刚性反向涡动) 频率不断下降( 甚至趋于0) ，而其章动( 刚性前向涡动) 频率不断升高。在对应于一阶弯曲模态的反向及前向涡动上，也能观察到类似现象，幸运的是，即便转子运行于400 Hz 转动频率下，其一阶弯曲反向涡动频率依然明显高于其同步频率，则在整个工作频率范围内，可将转子视为次临界运行的转子。当然，由于弯曲频率并未远离转子工作转速范围，在进行轴承控制器设计时，其振动的有效阻尼依然不能忽略。

图3 转子Campbell 图

2、分子泵转子与直流电机的耦合模态振动

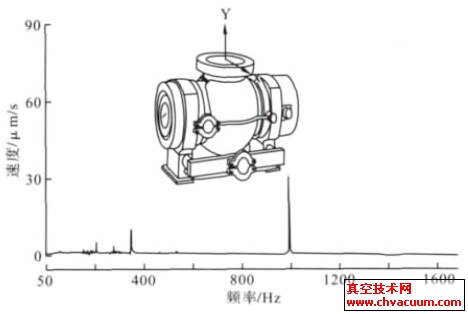
　　分子泵装备的电机为2 极永磁直流电机。电机转子为2 片永磁瓦，通过不锈钢套固定到转子芯轴上。电机转子永磁材料稳定性不够，经历数个小时工作转速下的初始运行后，其永磁铁上剩磁发生变化，并且变化不均匀。这时，一种奇怪而危险的模态振动开始显现，对转子位移传感器信号进行FFT 分析，查看其频谱，能观察到220 Hz 附近出现了一个振动峰，且此振动峰在下径向传感器处尤其明显，如不及时停机，该峰不断上涨，最后会导致转子失稳。对新的分子泵转子，此峰首次出现后，停机再次运行时，当转动频率高于350 Hz，下径向位移频谱上该峰会自行出现，并随转速提高及运行时间累积而愈发明显。而在转子静态悬浮，或者低速运行时，却完全观察不到它。甚至在磁轴承中添加正弦扫频信号,通过磁轴承进行单一频率振动激励，也难以将它激发出来。当转速不断提高，同频高于280 Hz 后，却可通过扫频信号找到对应的振动峰。

　　当转子到达其最高工作频率400，220 Hz 的模态振动刚开始还稳定。几个小时后，对应此模态的位移FFT 峰值会缓慢而持续地增长，最终导致转子失稳。

　　这个现象的合理解释依然没有找到，但是可以通过实验探索其根源。可以肯定的是，此模态不是来源于泵壳体或是涡轮叶片。它与电机转子永磁铁的状态紧密相关，并可与转子章动进行运动耦合。高速下运行时，转子章动频率会向220 Hz 靠近，这时候章动与220 Hz 模态振动甚至会耦合出一个新的特征振动，比如一个频率200 Hz 的振动。

3、控制器设计

　　对于一般的磁轴承控制器设计，有大量的工作围绕转子弯曲模态振动，或叶片颤振，或转子章动与进动展开。在此分子泵系统上，这些问题都存在，且伴有一个新的令人困惑的220 Hz 模态，这些问题必须同时解决，而针对这些振动的控制量之间往往存在冲突，控制器参数需要在各个振动的抑制效果上进行谨慎折中，于是控制器设计变得很困难。对于复杂的控制器设计，诸如H] 及L 综合等鲁棒控制方法很有吸引力。但是，对于工业应用场合，它们通常过于复杂，且为避免性能过于保守，依然需要精确的模型信息，并尽量准确地描述各种参数的不确定性。而对于此分子泵系统，仅220 Hz 模态的信息就很难提供，再考虑工业应用的实际情况,鲁棒控制方法难以采用。因而，在磁轴承控制器设计中，更多考虑了相位整形方法。这种方法核心思想是通过向一个基础控制器中添加不同种类的滤波器，改变其局部频率范围的幅频及相频特性，以在相应频率域对模态振动进行有效抑制。这些滤波器通常添加到一个PID 控制器中，以改变PID 控制器的局部频率范围的振动抑制性能。滤波器的参数可以根据所需抑制的模态振动的不同，方便地进行调整。

3.1、弯曲模态振动抑制

　　对于运行转速超过或接近其弯曲模态频率的磁轴承转子而言，弯曲模态振动的抑制必须充分考虑,否则当存在弯曲频率附近的振动成分，比如不平衡激振力，弯曲模态振动很容易被激发出来。虽然此分子泵转子为次临界转子，其一阶弯曲模态振动依然需要进行抑制。通过相位整形方法在磁轴承PID控制器中添加相应的整形滤波器，可以有效提高对弯曲模态的阻尼。这里所采用的相位整形滤波器为二阶陷波器，其伯德图如图4。通过向径向磁轴承控制器中添加此滤波器，可以有效修正一阶弯曲频率范围附近的控制器增益与相位特性，明显改变原有PID 控制器对弯曲模态的阻尼特性。控制器在一阶弯曲频率附近的相位会明显增加。添加滤波器后，即便一阶弯曲模态后向涡动频率因陀螺效应随转速下降，控制器依然可以为一阶弯曲振动提供阻尼。

图4 用于一阶弯曲模态的整形滤波器伯德图