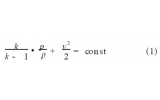双活塞缸式气动真空发生器的理论模型研究

　　本文依据前期的实验研究结果，将双活塞缸式气动真空发生器的活塞运动过程简化成匀加速、匀速、匀减速3个运动过程，得到了活塞运动速度与系统参数之间的关系，推导了不同运动阶段被抽取的真空容器内压力变化的近似解析表达式，并采用热量补偿的方法对热交换过程的影响及时地进行修正，通过累加计算，得到了真空容器及吸盘的真空响应过程。

引言

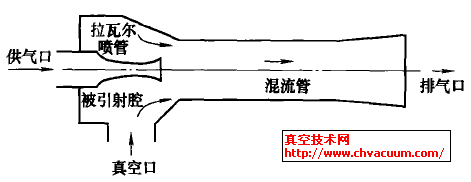
　　随着工业自动化生产线中对控制要求日趋严格，需要比较精确地得到真空抽气系统启动后，吸盘处的真空响应时间。本文介绍的双活塞缸式气动真空发生器工作原理如图1所示，它能在相对较低的供给压力下迅速达到一般工业上需求的真空度，并且耗气量相对较低，有利于气动系统节能。

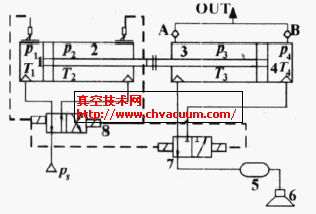
1—动力腔Ⅰ　2—动力腔Ⅱ　3—真空腔Ⅰ　4—真空腔Ⅱ　5—真空容器　6—真空吸盘　7—吸气换向阀　8—驱动换向阀

图1　双活塞缸式气动真空发生器工作原理

　　在真空技术网另文中已建立其数学模型，它是一个微分方程组，通过模型数值求解可以得到各腔室压力变化及运动情况，但是并不能清楚地表示各参数与系统性能指标之间的关系，为了能够更加深入了解它们的内在联系，加快求解速度，通过本文的研究，希望能够得到真空吸盘的压力变化过程与系统结构参数相关的近似解析表达式，便于进行结构优化。

1、运动过程分析

　　活塞在一次抽气行程中，真空容器内的压力变化如图2所示。活塞启动后，真空腔室和真空被抽容器行程的密闭容积逐渐扩张，使压力降低，直到接近行程末端时，抽气换向阀换向，另一真空腔室内的部分气体回流到被的真空容器中，造成压力略有上升，在下一个行程活塞反向运动时，运动规律基本一致，这与试验测得的压力变化过程是相同的。

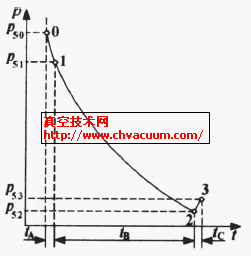
图2　一个运动行程内真空容器的压力变化过程

　　通过前期的试验研究，测得了系统在多组供给压力和流量下的运动情况，图3为在如下参数时试验测得的活塞运动速度曲线：动力腔直径30mm、真空腔直径40mm、活塞杆直径8mm、供给压力0.21MPa，平均供给流量56L/min，在不同入口真空度时的活塞运动速度形状大致相同，只是波动的幅度略有不同。从图3中可以看出，活塞在开始一段为匀加速段，中间处于一个相对变化较小的平台段，末段为匀减速段(活塞反向运动规律也大致相同)。为了简化计算，我们假定将一个运动行程内活塞的运动速度分成以下3个阶段：匀加速运动、匀速运动和匀减速运动，3个阶段的运动时间分别为tA、tB、tC，运动位移为X1、X2、X3，满足行程关系S=X1+X2+X3。

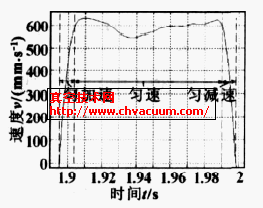
图3　一个运动行程内活塞运动速度变化

　　根据真空技术网(http：//www.chvacuum.com/)的研究，质量流量公式可简化成

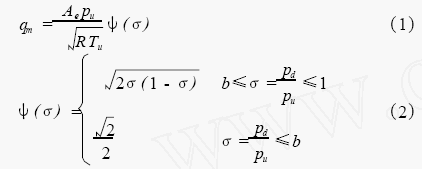
　　式中：pu、pd为上、下游绝对压力，Pa；

　　Ae为流道等效流通面积，m2；

　　R为气体常数；

　　Tu为上游绝对温度，K。

　　以气源向动力腔Ⅰ供气、活塞向右运动为例，其流量还可表示成

　　因此，根据流量连续性关系得

qm1=q′m1(4)

　　并且，根据测得的腔内气体压力变化情况以及活塞的运动速度大小，气体流动过程基本是处于亚声速流动状态，所以

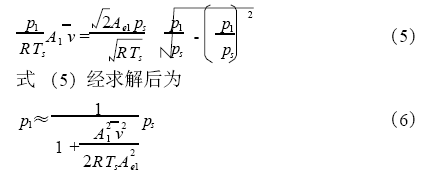
　　再将式(6)代入式(3)，即得到动力腔供给流量与供给压力、平均速度、结构参数之间的关系，如式(7)所示。

　　因此，活塞的稳定运动时的平均运动速度v也可用供给压力和流量及相关参数表示

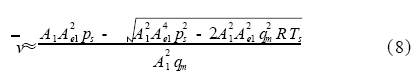
　　式中：ps为气源供给压力，Pa；

　　A1为动力腔Ⅰ工作面积，m2；

　　Ae1动力腔Ⅰ进气流道等效面积，m2。

　　2、热交换的影响

　　双活塞缸式气动真空发生器在抽取真空的过程中，并非在很短的时间内将被抽取容器内的气体抽出达到一定的真空度，而是一个逐渐抽取的过程，同时也伴随着被抽取容器内气体与外界的热交换过程。所以，在推导真空容器内压力变化时，必须考虑热交换过程的影响，并及时地对气体参数进行修正，这样才能使得到的结果更加接近实际情况。

　　根据热力学第一定律和气体状态方程，可以按绝热容积扩张过程求得被抽取容器内的压力p′以及温度，单次抽取真空过程时间约为0.1s，所以可先以绝热过程推导的温度与外界温度之差在过程时间内吸取的热量作为该运动过程的吸热量，再对压力、温度进行修正，通过这样的方法来近似模拟实际抽气过程，计算过程如图4所示，0→1′→1→2′→2→3′→3。

　　参与热交换的这部分热量流入到真空容器中后，引起的温度变化量可由式(9)计算。

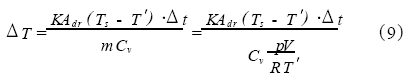
　　所以，对真空容器内的温度和压力进行修正后为

3、真空压力变化过程研究

　　3.1、匀加速运动

　　同样，我们以活塞向右运动过程为例对真空容器内压力变化进行分析。匀加速运动阶段是在活塞反向运动启动后出现的，该过程的加速过程时间短、位移小，通过统计多组不同结构参数下测得的实验数据，该过程的位移约为3mm，活塞的运动速度为：

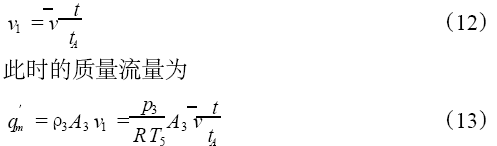
　　再结合流量计算公式(1)、(2)和流量连续性关系(4)，最后可求解得到真空容器压力与抽气腔室压力的关系式，见式(14)。

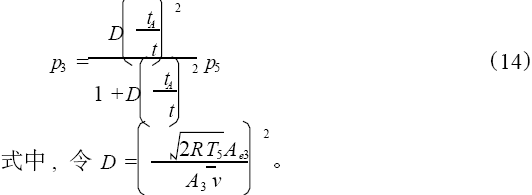
　　当完成匀加速运动阶段后，即t=t0+tA时，根据质量守恒方程，原真空容器中的气体质量m应等于抽取后真空容器内气体质量m1与抽气腔室内气体质量m2之和，即：

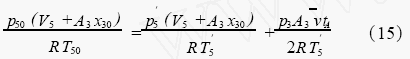
　　以绝热容积扩张过程进行计算，可得被抽容器内的温度为

　　考虑该阶段运动时间内，真空容器与外部的热交换的影响后，应对温度和压力进行修正，代入式(9)—(11)后所得到的p5和T5即为匀加速过程结束时真空容器内的压力和温度，同时也作为下一匀速运动阶段的起始参数。

　　3.2、匀速运动

　　在这一阶段，同样根据质量流量连续性方程和质量守恒程，可以推导出在完成该阶段运动过程，即t=t0+tA+tB时的各参数的关系式：

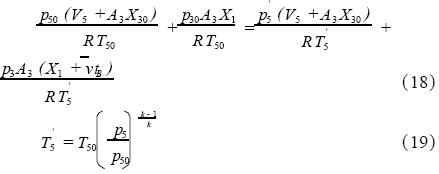
　　同样，在该阶段考虑热交换的影响后，对温度和压力进行修正，代入式(9)—(11)计算得到修正后的p5和T5为匀速运动阶段结束时真空容器内的压力和温度，同时也作为下一匀减速运动阶段的起始参数。

　　3.3、匀减速运动

　　当活塞运动到接近行程末端时，触发充气换向阀和抽气换向阀换向，气源气体开始流入动力腔Ⅱ，使活塞减速运动，该过程的运动行程为换向阀的切换行程。在这个过程中，抽气换向阀换向后，被抽的真空容器与真空腔Ⅱ相连，真空腔Ⅱ内的气体压力应为p0+Δp，Δp为单向阀的开启压力，大于真空容器内气体压力，必定回流到真空容器中去，所以，当活塞运动到行程终点时的质量守恒方程为：

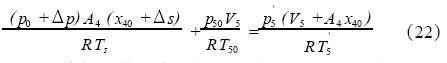
　　再将相应的温度变化关系式(19)代入式(22)后求解，得到活塞运动到行程终点，即t=t+tA+tB+tC时真空容器内的压力为：

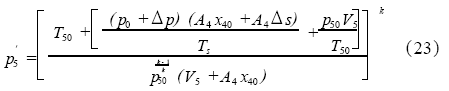
　　然后，再将求得的p′5、T′5代入式(9)—(11)进行修正，得到的p5、T5为匀减速阶段完成后真空容器内的压力和温度。

　　以上计算过程将活塞的运动过程分为3个阶段，并且将实际的热交换过程通过温度、压力修正的方法进行处理，每个阶段所得到的压力与时间相对应，这样就可以近似得到一个抽气行程内真空容器压力变化情况。当活塞向左运动时，计算过程基本类似，将不通的参数值代入对应的方程即可，通过这样不断地将往复抽气过程进行叠加，可得到我们所需要的真空容器内的压力变化情况，并且给出的计算式中与结构参数和工作参数相联系，能够更好地表示它们之间的互关系。

　　以上从理论上推导得出了单个抽气过程中真空容器压力变化过程，还需通过实验对之进行验证，以确定理论推导的正确性，比较实验结果与理论计算的差异。

4、模型验证

　　在理论分析的基础上，笔者对多组动力腔直径、供给压力、供给流量的样机模型进行了实验，将测得的真空容器压力与理论计算结果进行对比，图8为部分对比结果，对应的实验参数见表1。

图8　不同参数下真空容器真空度与理论计算对比

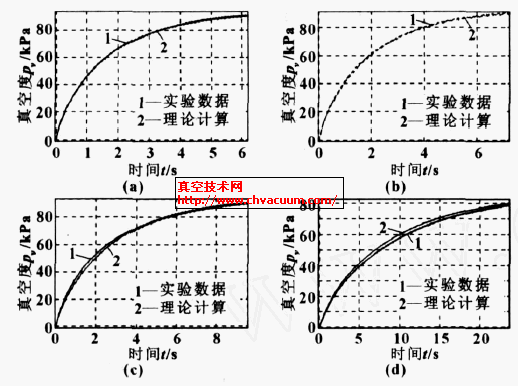
表1　图8中各组实验参数

　　通过图8中的对比可以看出，在不同参数下实验数据与理论计算值在线型和数值上误差均较小，理论计算基本上能够反映出实际真空容器内的真空压力变化过程，说明上述的推导过程是可靠的。

5、结论

　　通过对双活塞缸式气动真空发生器前期实验研究，将活塞在单个行程内的运动过程简化为匀加速、匀速、匀减速运动，推导出活塞运动速度与系统结构参数和工作参数之间关系，并采用能量补偿的方法对抽气过程实际热交换的影响进行修正，得到了真空容器压力变化过程的近似解析表达式及其真空响应过程，更加明确了各参数对真空响应过程的影响。最后，采用实验的方法进行了验证，结果表明，理论计算结果与多组参数下的实验情况都较为符合，证明了采用文中的假设和推导过程是可行的，可为进一步的优化设计提供了依据。