磁性液体密封结构的优化设计
在磁性液体密封的理论及现有设计原则的基础上,建立了以磁铁体积最小和极靴长度最小为目标的密封结构优化设计的数学模型。利用带有约束条件的多目标混合遗传算法,通过Matlab 编程与Ansys 软件的交互运算,实现了对密封结构的优化设计。结合具体实例的计算结果并与初始值的比较表明,在保证密封耐压的前提下,优化后的结构参数可以使磁铁体积减小74.7 % ,极靴长度减小5.45 % ,漏磁减小84.5 %。
磁性液体密封的设计通常以耐压能力为主要设计目标,而耐压能力取决于密封间隙内的磁场和磁性液体的磁化特性。密封结构与参数对密封间隙内磁场有决定性影响,如何在给定密封耐压下最优设计密封结构尺寸,以减小其体积,降低密封装置成本,是现今密封装置设计的重要问题。Oscar Pinkus等在理论推导和实验总结的基础上给出了部分结构尺寸的选定范围,但这对总体结构尺寸的确定尚不全面。邹继斌、赵国伟等从材料选取和结构设计方面给出了磁性液体密封的设计原则,但对结构参数只给出了经验的选取范围,对某一具体结构并没有细化到其最优值。孙明礼等针对具体结构,在其它条件确定的基础上,对密封齿形进行了优化设计,这种方法能够找到特定条件下的最优齿形参数组合,但对整个结构参数的确定来说不够全面。
遗传算法是基于自然选择和自然遗传这种生物进化机制的搜索算法。其对问题的优化过程与生物一代一代的自然进化相类似,它对由多组自变量组成的群体不断地进行选择、交叉和变异操作,并按照优胜劣汰的规则,将较优的自变量组合遗传到下一代,最终在群体中得到最优的自变量组合。遗传算法具有较高的搜索效率,并能够减少搜索过程陷于局部最优的风险,且对目标函数几乎没有限制,具有较强的适用性 。
本文在前人工作的基础上,采用多目标混合遗传算法,在保证耐压指标的约束条件下,对具体密封结构进行优化设计,找到使密封装置体积最小,成本最低的最优结构参数值。
1、磁性液体密封结构优化的数学模型
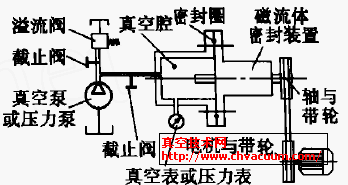
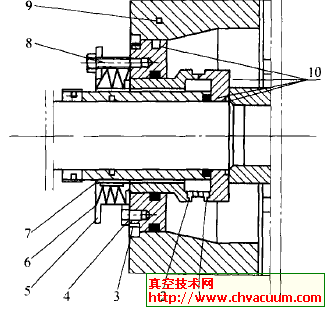
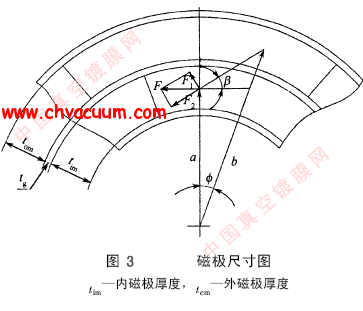
密封结构的设计中,在满足密封耐压的前提下,人们总是希望设计出体积小、成本低的密封装置。如图1 所示的典型磁性液体密封结构中, 轴的半径r 是由密封对象决定的, 整个装置总的半径t 受限于所选择轴承的外径, 同时又可根据设计经验及耐压指标确定所设计的齿数n 。所以优化设计中以极靴的轴向长度最小和磁铁的体积最小为目标函数。设计参数分别为:密封间隙lg , 齿宽lt , 槽宽ls , 槽深lh ,磁铁长度L ,磁铁宽度s ,磁铁内径R 。

图1 典型磁性液体密封结构
极靴轴向长度的目标函数为
![]()
磁铁体积目标函数为
![]()
根据真空技术网前文中的讨论,某一级的密封耐压值近似为
![]()
其中μ0 、Ms 、Hmax和Hmin分别为真空磁导率,磁性液体的饱和磁化强度,密封间隙内某一齿下的磁场强度的最大值和最小值。这样在所有的设计参数下,必须满足的耐压条件为

其中CP 为给定的耐压指标。当选定磁性液体后,其饱和磁化强度为定值, 这时密封耐压值可用各齿下的磁化强度差的极大值来衡量, 所以耐压条件可以转变为:

式中Hc 为耐压达到所要求的指标时对应的各齿下的磁化强度差的和的极大值。
综上所述, 并根据磁性液体密封的设计原则 ,可得密封结构优化的数学模型为:

式中X = [lg,lt,ls,lh,L,s,R]T , F 为带有两个目标函数的矢量。式中数值的单位为mm。
2、带约束多目标混合遗传算法的实现方法
本文对密封结构的优化采用目标权重和的遗传多目标优化方法。该方法是给定每个目标函数的分配权重,然后将加权目标结合为单一目标函数。由于不能明确区分密封结构中极靴轴向长度和磁铁体积孰重孰轻, 所以在遗传算法中, 采用随机权重方法,即起初遗传搜索向着Pareto 解的前沿进行, 此后随着进化的进行,适应性地随机调整权重,这样可保证群体对搜索方向的多样性。目标权重和函数为
![]()
其中, w1 、w2 为权重系数,且w1 、w2 > 0 , w1 + w2 = 1。在优化程序中,随机权重系数按下式计算:

ζ1 ,ζ2 为计算机产生的随机数。
由于密封间隙内磁场只能通过数值方法进行计算,因此我们调用专业的磁场计算软件Ansys 来实现磁场分布的计算,密封结构模型的建立等操作都通过APDL 编程在Ansys 中完成,完成计算后Ansys将计算结果返回给优化程序。另外,为了增强遗传算法的局部搜索能力,在遗传算法中嵌入局部贪婪性搜索过程。为了保证在每一代进化中不遗失较优解,采用定义非受支配解集合的保优策略。总的优化步骤为:
(1) 随机产生M 个初始个体,形成初始群体;
(2) 计算各个体的适应度值并调用Ansys 计算磁场分布,对不满足耐压条件个体的适应度处以罚函数;
(3) 判断所有个体是否都不满足耐压条件,若是,则返回步骤(1)重新产生初始群体;
(4) 按适应度大小进行排序,并将适应度最大的前N 个个体存入非受支配解集合;
(5) 计算随机权重系数和除非受支配解外的M-N 个个体在新的权重系数下的适应度;
(6) 采用比例选择的方法进行选择运算,然后经交叉和变异运算后形成新的群体;
(7) 对新群体中的个体及非受支配解集合中的个体执行局部搜索操作得到M 个个体组成的群体;
(8) 算法终止判断,若满足终止条件,则输出结果,否则转到步骤(2)。