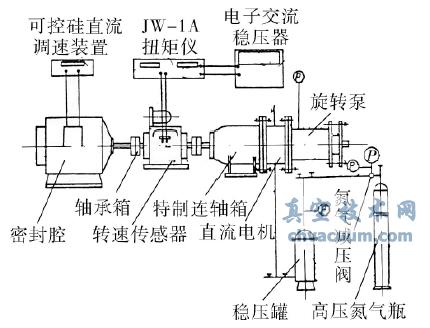
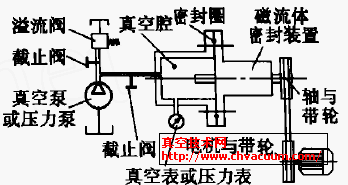
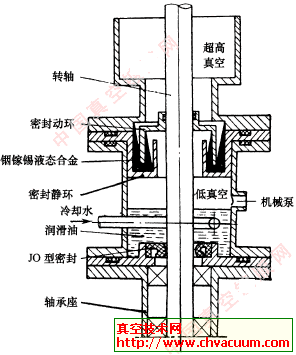
磁力传动真空动密封在超高真空设备上的应用
1、超高真空设备用磁力驱动器的特点
在磁力传动技术中各种磁力传动器的基本工作原理是相同的。但由于应用领域的不同,用于不同场合的磁力传动器又各有其自身的特点。
所以对特定环境下使用的磁力传动器进行专门的研究是必要的。用于超高真空设备上的磁力传动器与普通的磁力传动器相比较其最大差别,就是内磁转子上的磁体不使用永磁性材料而是用软铁材料所取代。这是因为超高真空设备为了获得超高真空,在抽气过程中,必须对设备的真空室进行烘烤去气,如果内磁转子采用永磁性材料,会因烧烤温度超过永磁体的居里温度而使永磁体退磁失效。因此不得不采用不怕烧烤的软磁材料。而外磁转子在烘烤去气时又可从设备上拆下或采取一些保护措施,因此不会受到影响。内磁体通常可采用软磁性材料来代替。由于这种材料的更替从而导致了工作原理有所不同,致使其
工作特性曲线发生变化,为此对超高真空设备上所使用的磁力传动器进行专门的研究是必要的。
2、超高真空设备用磁力传动器的原理及结构
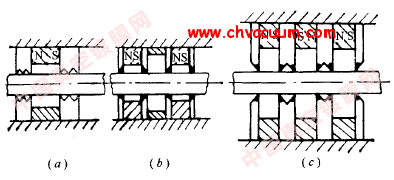
超高真空设备用磁力传动器的基本原理是基于软磁材料在靠近永磁体的磁场时会被感应磁化并受到吸引力作用的这一现象而实现的,它的具体结构通常是在要求运动传递的部位设置一个筒形静密封隔离套,将真空内外隔离,当按照适宜磁路结构合理排列的永磁体在筒外作旋转或直线往复运动时,筒内对应位置的软磁材料受其吸引力作用也随之运动,并带动与之相关联的部件,从而实现向真空室内传递运动的作用。筒内的软磁材料通常采用磁导率和饱和磁感应强度均较大的纯铁,外磁筒中的永磁体,一般选用矫顽力高的永磁材料。如钕铁硼材料。为了充分地利用磁能提高传递转矩,减小元件体积和降低成本,永磁体的形状和排列方式都应进行精心的设计,并用导磁材料组成闭合回路。超高真空设备中常采用的磁力传动装置有旋转运动式、往复直线运动式等磁力传动器,其结构如图12、图13 所示。
图中虚线表示磁通环路。由于超高真空用磁力传动器手动式较多,因此图12、图13 中没有给出内磁套及支撑元件,而是将其直接放入到隔离套内。当要求推进器同时传递旋转运动时,只需将磁力转轴的结构简单地串联在一起即可。

图12 超高真空设备常用旋转运动式磁力传动器的结构示意

图13 超高真空设备常用往复直线运动式磁力传动器的结构示意
图14 物理模型示意图
3、超高真空设备用磁力传动器结构参数的优化
为了使超高真空设备用磁力传动器,达到结构性能参数的要求,对传动器进行结构参数的优化是十分必要的。
① 物理模型
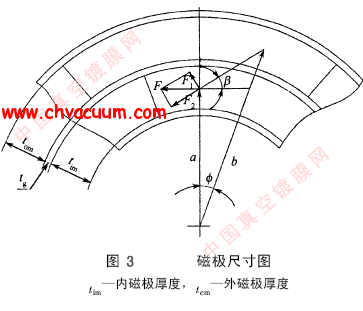
由于磁力传动器的径向气隙尺寸远小于轴向尺寸,故将磁场分布简化成二维平面磁场问题。基于磁路结构的对称性、周期性[5],同时为了更准确地反映出磁力传动器内部磁场相互作用的实际情况,可以半个圆周为研究对象。建立起图14 所示的物理模型,具体结构参数见表3。
② 数学模型
采用矢量磁位A 作为求解对象,利用有限元法求解场的拉普拉斯方程的边值问题,就是把该边值问题等价为一个相应的条件变分问题,通过引入近似函数,把条件变分问题离散为方程组,最后求解方程组,求得磁场的分布后,再用麦克斯韦应力法求得最大转矩。
表3 物理模型结构参数

③ 结构参数优化
利用有限元法对磁力传动器的极间角α,齿长L,永磁体厚度hm,极数m 等参数进行一系列计算,从中算出了最佳参数。计算中选取外转子轭铁外径为100 mm 的传动器作为结构基本模型,外转子的轭铁及内转子的材质为纯铁,外转子的永磁材料为NeFeB37MGO。
a 极间角α 的优化如表4 所示,对于m=6的传动器,永磁块的弧度角β=60°,当内磁转子轭铁的极间角α=48°时,转矩最大;对于m=12的传动器,永磁块的弧度角β=30°,当内磁转子轭铁的极间角α=24°时,转矩最大;对于m=16 的传动器,永磁块的弧度角β=22.5°时,当内磁转子的轭铁的极间角α=18°时,转矩最大。由此可见,传动器的最优极间角与永磁块的弧度角有关。表4 的三组数据表明,α=0.8 β 时为最优极间角。
表4 极间角α 与转矩T 的关系

b 齿长L 的优化齿的长短对转矩的大小有影响,而齿长对转矩的影响与永磁体的厚度有直接关系,从表5 可以看出:齿长的最优值为略大于永磁体的厚度。
c 外磁转子轭铁厚度hi 的优化沿径向磁化的磁体组成的磁力传动器,外轭铁的使用能明显地提高磁力传动器的性能,轭铁的厚度对转矩的传递也有影响。如果轭铁的厚度太薄,在轭铁处将出现如图15 所示的磁饱和使磁阻增加,气隙磁密减小,传递的转矩降低,磁力传动器的性能下降;如轭铁的厚度太厚,对传动转矩的增加并无太大贡献,但却使旋转部件的转动惯量增大,从而增加了传动器的启动转矩,降低了磁性材料的利用率,使运动部件的不稳定性增加。两组反映轭铁厚度hi 与传递转矩T 的关系的计算数据见表6。由表6 可知:轭铁的厚度取永磁体厚度的1~2 倍为好。而Δr(Δr=r1-r2)值对转矩的影响不大。
表5 齿长L 与转矩T 的关系

表6 轭铁厚度hi 与传递转矩T 的关系

d 永磁体厚度hm 的优化在保证轭铁不饱和的情况下,进行了多组不同永磁体厚度的转矩计算数据见表7。在一定范围内(3 mm~7 mm),随永磁体厚度的增加,转矩增加得较快,超过此范围,转矩增加得较慢。这是因为磁体随厚度的增加,磁势增加,而磁阻、漏磁也随着增加,当厚度增加到一定值后,所增加的磁势几乎全部消耗在增加的磁阻、漏磁上,而对外磁路的贡献很小,所以出现了永磁体厚度增加很多,而转矩增加很小的情况。基于上面的分析,为了提高永磁体的利用率,永磁体的厚度不宜太厚。
表7 永磁体厚度hm 与转矩T 的关系

e 永磁极数m 的优化不同极数下的转矩值见表8,从表8 中可以看出极数太少或太多对转矩的传递不利,由静磁能的表达式:
式中EH—— —静磁能;H—— —磁场强度;J———磁体的磁耦极矩;m———磁极数;φ———内、外磁转子的角度差。
表8 永磁体的极数m 与转矩T 的关系

可以看出极数多有利于静磁能的储存,静磁能最终被转化为动能而被释放,所以说极数多,有利于转矩的传递,但极数太多,从图16 中可以看出磁块之间漏磁太多,不利于转矩的传递。所以极数的选取应适中,本计算所用磁力传动器12极为最佳。

图15 轭铁处磁饱和磁场分布
图16 多极数时磁场分布
推荐阅读: