柱塞密封结构的漏率预估
柱塞密封结构是飞船管路系统常用的一种密封结构形式,故研究柱塞密封结构的密封性能具有重要的工程意义。文中,通过对柱塞密封结构密封机理的分析,给出了一个计算其漏率的理论公式,并与试验数据进行了对比。研究结果表明:该公式能较好地预估柱塞密封结构的漏率值。本文所得的结论可以为柱塞密封结构的设计提供理论参考依据。
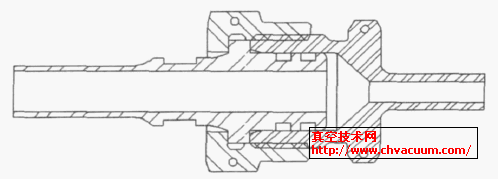
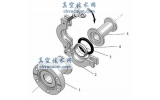
密封是工程领域永恒的课题之一,为满足实际工程的需要,人们研究出不同的密封技术,如磁性液体静密封技术[1]等。在航天工程领域,柱塞密封结构由于具有良好的密封性能,因而被广泛用于飞船各个分系统的管路连接中,如返回舱的推进系统、轨道舱的环控系统和内回路系统等。因此,研究柱塞密封结构的密封性能具有重要的工程意义。柱塞密封结构的示意图见图1 ,其密封的机理是两个橡胶O形圈的串联密封。其实,橡胶O形圈密封结构的研究历来是学术界研究的热点问题之一,其研究的文献可参考[2-5] 。这些文献都有一些共同的特征,即通过建立O形圈的简化模型,利用各种方法(主要是有限元) 计算出O 形圈密封结构在工作状态下的变形和应力,以及密封面的密封状态,如密封宽度、最大密封应力、平均密封应力等,却鲜有人研究反映密封面密封状态的量与漏率的关系。
同时,在实际工程中,由柱塞密封结构的几何尺寸即可确定橡胶O 形圈的压缩率(25 %) ,那么已知了橡胶O形圈的压缩率,能不能就能预估出柱塞结构的漏率呢? 本文即尝试在建立密封面上密封状态的量与漏率的关系的基础上,对柱塞密封结构的漏率进行预估。

图1 柱塞密封结构的示意图
1、单个橡胶O形圈密封结构的密封机理分析
1.1、漏率模型的建立
由于柱塞密封结构的双串联橡胶O 形圈是对称的,因此为简便起见,先研究单个橡胶O 形圈的密封形式,最后再推广到双串联橡胶O 形圈的密封形式中去。
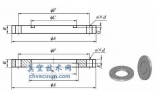
图2 橡胶O 形圈密封示意图 图3 橡胶O 形圈的主密封面示意图
单个橡胶O 形圈的简化密封示意图见图2。图中的主密封面是主要的泄漏通道,故本文仅考虑主密封面的泄漏情形。
据Roth[6 ]等的研究结论可知:两个表面通过压紧形成微米量级的通道,这些通道构成了密封面的泄漏路径。1967 年,A Roth 对机械加工表面进行统计测量,得出了表面沟槽90 %以上的峰值有α= 10~40 的斜率,他定出泄漏路径横截面的典型形式为底角α= 40 的等腰三角形,泄漏通道的长度等于密封面的宽度。据此,可假定在主密封面的不锈钢一侧的表面存在着横截面积恒定、底角α= 40的等腰三角形,长度为W 的三角形柱体孔洞。这样,密封结构的漏率就是n 个这样的三角形柱体孔洞并联而成的。若初始的三角形柱体孔洞横截面底边上的高为H ,则当密封结构中安装橡胶O 形圈后,由于橡胶材料的高弹性,将使H 减小为h ,从而大大提高了此密封结构的密封性能。当橡胶O 形圈的压缩率越大,截面的高度h 就越小,从而密封效果越好。但同时橡胶O 形圈的压缩率越大,其老化的速度也就越快。因此,在工程中,往往选择一个适当的压缩率[6] 。
因此,对于橡胶O 形圈密封结构,其泄漏的漏孔是由若干横截面积恒定且形状为等腰三角形的微型漏孔并联而成的。
1.2、漏率的理论预估
由于柱塞密封结构的总漏率要优于5 ×10 - 7 Pa·m 3 ·s - 1 ,而总漏率又是由若干小的漏孔并联而成的,故每一个小的漏孔的漏率必然远远小于5 ×10 - 7 Pa·m3·s - 1 。因此对于这些单个漏孔的气流状态均可认为是分子流。
在分子流状态下,漏孔流导的计算公式[6]为

式中, K、A 、B 、W 分别为形状修正系数,流道的截面积、包围流道面积A 的周界以及漏孔的长度。€v 表示气体分子的平均速度,由下式可以计算出

式中, R 为通用气体常数, T 为气体的绝对温度, M表示气体的分子质量。
对于单个横截面积上底角α= 40 , 底边上的高为h ,长度为W 的三角形柱体漏孔的流导, 可通过式(1)得到

对于直径为D 如图2 所示的密封结构,其主密封面上漏孔的个数n ,可通过几何关系得到

式中, H 为初始微型漏孔横截面底边上的高。由式(3) 、(4)可得,整个密封面的总流导为

由文献[7]可知

式中,σm 为密封面上的平均应力, Ks 为反映密封面上较软材料密封性能的系数。
将式(6) 代入式(5) 可得总流导为

故总漏率

式中,Δp 为漏孔两端的压差。上式在化简过程中将形状修正系数K = 1.7 ,α= 40 代入了。由上式可见,橡胶O 形圈密封结构的漏率与压差,气体的分子量、温度,密封结构的直径,密封面的粗糙度以及密封面的状态均有关系。若密封面的表面粗糙度越低,密封面上的平均应力越大,那么密封性能就越好。