干式气体端面密封的研究现状
对非接触式干式气体端面密封(DGS)的研究进展进行了总结, 着重介绍了密封性能的理论分析与数值计算方法, 端面微槽的优化设计方法,试验研究方法以及考虑端面微尺度效应和滑移流效应基础研究等方面的研究现状。指出在高参数条件下DGS端面的热流固耦合与解耦分析, 低速或低压条件下密封的启动与停车性能的准确预测及结构优化是DGS技术未来研究的重点,也是进一步拓广DGS应用领域、提高其工作可靠性的关键。
干式气体动力润滑机械密封(DGS)是在止推轴承技术的基础上, 通过在密封面上开槽并以气体作为润滑剂的机械密封。开槽使密封面旋转时产生了流体动力效应, 实现了密封面的非接触, 同时端面间剪切流对抗压差流达到零泄漏。DGS的研究与应用已有30余年, 目前已在石油、石化、化工和电力等部门得到越来越多的应用。随着DGS应用于高参数场合或低速、低压场合, 新的问题不断出现, 因此对DGS提出了更高要求, 了解有关DGS的基础知识、研究现状和发展趋势, 提出解决或部分解决上述类似问题的方法, 完善DGS的设计理论与设计方法和实验研究方法, 具有重要的理论价值和实际意义。
1、DGS的结构和密封机制
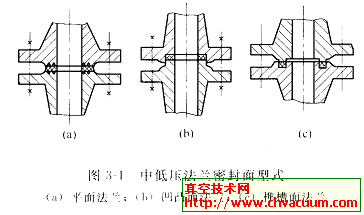
除密封端面开有各种不同型槽外, DGS和普通机械密封一样由静环和动环组成。DGS的型槽形式多样, 常见的有圆弧槽、螺旋槽、直线槽、T型槽、枞树型槽等, 槽深一般为3~30μm。
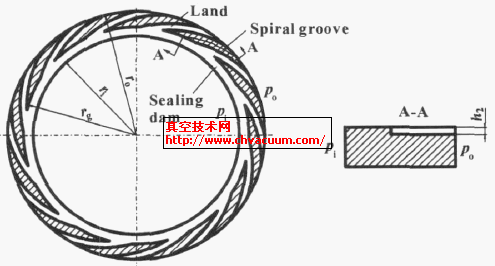
图1 S-DGS的端面结构示意图
图1所示为典型的螺旋槽DGS(S-DGS) 端面。当密封工作时, 气体被吸入槽中, 其流动受密封坝节制, 于是气体被压缩引起压力升高, 该压力企图使密封面分离, 并形成一定厚度的气膜。当气体压力和弹簧力与开启力平衡时, 形成稳定的气膜并防止密封面相互接触。气膜厚度一般为几个微米。
图2所示为S-DGS的作用力图。作用于浮动密封环上的闭合力为Fc , 其值等于系统压力和弹簧力之和, 设开启力为Fo, 其值等于气膜承载能力的大小。当Fc = Fo 时, 密封处于稳定运转状态, 为理想的设计工况; 当DGS受到外来干扰气膜厚度减小时, Fc保持不变, 而型槽产生的端面动力会明显增大使Fc< Fo ,导致膜厚增大, 恢复到原值; 相反, 当外来干扰使膜厚增大时, 端面动力下降使Fc > Fo,密封面合拢恢复到原膜厚值。这样, 动、静环间始终保持一层稳定的气膜, 在正常运转条件下, 两密封面始终保持非接触, 密封面无磨损, 从而提高密封寿命, 使密封可以长期稳定运转。
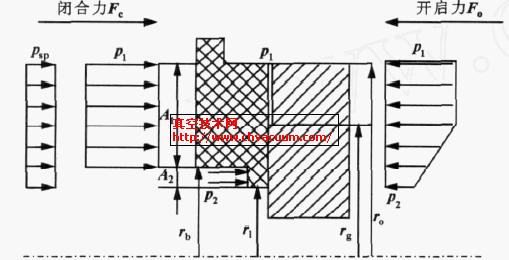
图2 DGS的作用力图
2、DGS的研究现状
DGS的理论基础来源于气体润滑理论和气体止推轴承理论。对DGS的研究主要采用理论解析计算、数值模拟和实验研究等3种手段, 目前数值模拟计算是最常用的手段。以Navier-Stokes方程为端面间气膜压力控制方程, 通过计算气膜压力、开启力、气膜刚度和泄漏量等密封参数, 对DGS进行优化设计并完善设计理论。
2.1、DGS性能的解析法研究
DGS的解析研究基础是Whipple提出的窄槽理论(Narrow groove theory, NGT) , 该理论后来得到了Malanoski等和Muijderman的完善, 其中Muijder-man首次采用复变函数保角变换理论将螺旋槽模型转化成平行直线槽模型, 并重点考虑槽端部的影响, 出了较完整的螺旋槽轴承理论。Cheng等运用NGT分析了S-DGS和瑞利台阶DGS中, 密封槽和密封坝的相对位置对密封性能的影响, 指出在低速情况下,密封坝在低压侧有利于减少泄漏, 在高压侧有利于提高气膜刚度。Gardner最早将螺旋槽近似解析理论应用于螺旋槽端面机械密封的性能。Sneck等提出了一种基于窄密封面沿槽线建立雷诺方程的解析方法, 但由于该方法的不严谨和不方便, 未能获得广泛应用。Shapiro等在Muijderman方法的基础上, 考虑惯性力的影响, 研究了高速液氧泵用螺旋槽机械密封的工作性能。
2.2、DGS密封性能的数值模拟法研究
由于气膜压力控制方程很难直接求解, 所以解析法需作大量假设简化, 这给精确描述DGS的性能会带来一定的误差。随着计算机技术的不断发展和普及, 目前有限差分法(FDA)和有限元法(FEA)等数值分析方法已经在DGS的密封性能分析研究中得到广泛应用。
James等应用FDA研究了气体润滑螺旋槽平面推力轴承的性能, 并采用坐标变换法解决了螺旋槽曲线边界应用FDA所遇到的困难。Zuk等用FDA求解了模拟螺旋槽机械密封的直线平行槽模型的流场和压力场。Murata等利用势流理论, 建立了螺旋轴承的二维模型, 用数值分析方法计算了速度场和压力场。Smalley基于NGT理论, 用FDA求解雷诺方程, 计算了平面、球面和圆锥面等型槽气体轴承的承载能力、功率损耗、泄漏量和刚度系数。Lip schitz等用FDA计算了直线槽双向旋转气体推力轴承的性能。Kowalski等采用FDA分析了S-DGS的反转能力, 并通过坐标变换, 解决了螺旋槽的几何结构与柱坐标轴不一致造成的困难。
Reddi等应用基于伽辽金加权余量法的递增变分公式研究了气体动力轴承在低速情况下的稳态性能, 首次针对可压缩流体润滑问题采用FEA进行了研究。Ettles等用九节点二次等参元FEA求解雷诺方程, 获得了高的计算精度和较快的计算速度, 为DGS的数值分析计算提供了较好的算法。Satomi等采用FEA分析了低速气体径向止推轴承的结构参数优化问题。
Basu分别采用FDA和FEA研究了径向槽DGS的压力分布。Bonneau等采用基于伽辽金加权余量法的直接有限元公式对S-DGS进行了二维稳态分析,通过引入迎风格式, 消除了高速条件下计算结果的颤动问题。Tournerie 等将Bonneau等人的模型用于评价型槽的几何参数对低速、不对中S-DGS的开启力、泄漏量和回复力矩的影响。Hernandez等采用直接伽辽金有限元公式, 并结合对开槽面的特殊离散化程序, 确定了低速S-DGS的开启力、泄漏量和静力系数。Zirkelback等运用递增的伽辽金有限元公式, 计算了中、低速S-DGS的频率相关载荷系数。Ruan采用FEA分析了在低速、低压条件下, 滑移流对S-DGS密封性能的影响。Faria分析了高速S-DGS的性能, 计算程序以伽辽金加权余量法为基础, 同时引入了高阶形函数而无需引入特殊积分模型和人工分解, 所以具有精度高和速度快的特点。