体积比对静态膨胀法真空系统不确定度的影响
要使静态膨胀法真空系统测量不确定度达到10-3,体积比的测量是最关键的一步,墨西哥CENAM的体积比不确定度可以达到3×10-4 。
表1 不同路径对应的体积比
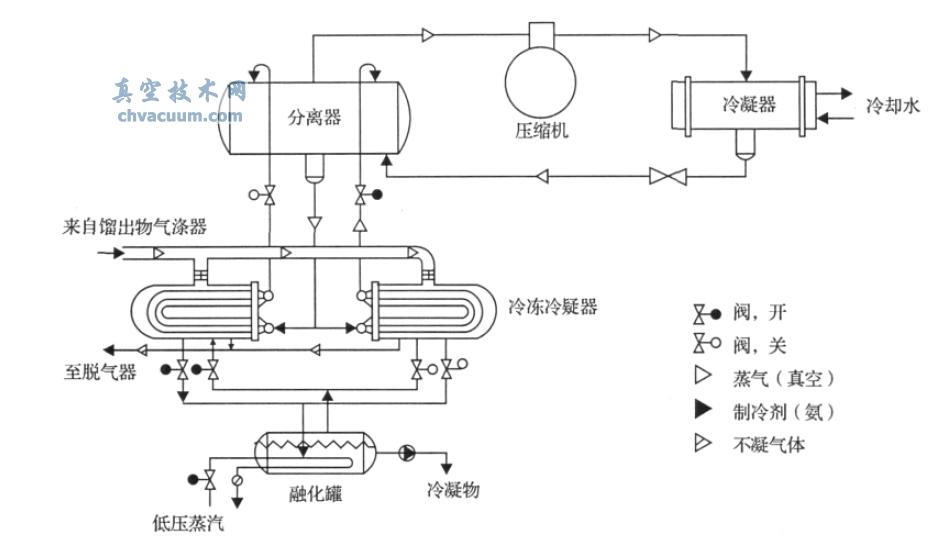
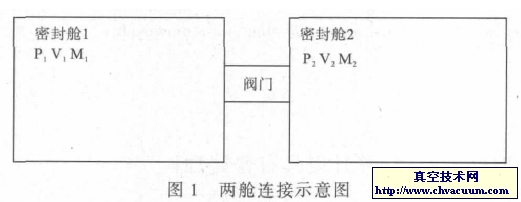
气体通过不同容积的小体积向大体积膨胀,可以获得不同体积比:通过v1或v2向大体积V1膨胀,以及v3向V2膨胀,分别得到10-2或10-3的压降率,不同的膨胀路径得到的体积比如表1所示。为了得到更大的压降,我们采用在I 级膨胀室循环多次的方法,可得到从10-2到10-9一系列不同的体积比。前级压力取样范围(104~105) Pa, 经过不同路径的膨胀,可得到(10-4~103) Pa的不同测量值。为了确定体积比值,我们采用灌水称重法来获得小体积的容积值,采用参考体积法来获得大体积的容积值。
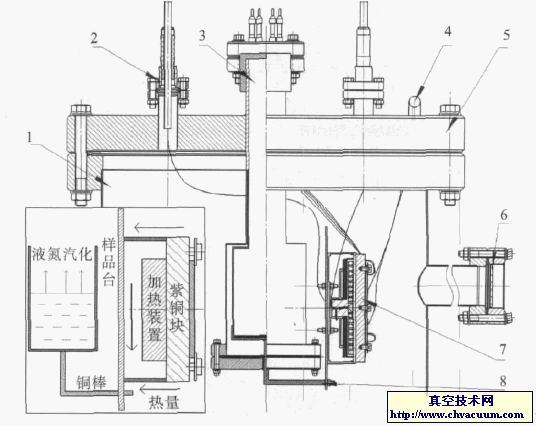
灌水称重法是一种绝对的测量容积值的方法,分别测量容器灌水前后的质量,通过计算质量差和水密度来得到容积值。称重使用的是分辨力为10mg的天平,用替代法称出小体积灌水前后质量,并同时测量实验室空气密度,进行空气浮力修正。用精度为0.01 ℃的温度计测量水温,得到相应水密度。用灌水称重法测得小体积容积结果为:
v1=0.772946L u ( v1)=2.1 ×10-5
v2=0.074663L u ( v1) =7.7 ×10-5
v3=0.752388L u ( v1) =3.3 ×10-5
称重法测体积在原理上可达到很小的不确定度,但由于大体积上连接很多管路和阀门,形状复杂,死角很多,灌水后很难使气泡排尽,复杂的结构也会使水温分布趋于复杂,这就是大体积用直接称重法的测量不确定度并不很小的根本原因。
例如PTB于1969年对约233升的大体积进行灌水的称重测量,其过程十分繁复,即使如此,测量不确定度也不过55mL, 即相对不确定度为2.3 ×10-4 。为了解决大体积的测量问题,我们设计了参考体积———约为大体积容积的1/4, 但结构单一且内表面光滑无死角,用灌水称重法测量参考体积的容积值,其相对标准偏差可以达到1 ×10-5 。再用参考体积通过单次膨胀的压力比法测出大体积的容积值,由于参考体积与大体积容积在同一量级,我们采用石英压力计的精确范围来进行压力测量,参考体积与大体积比值多次测量的相对标准偏差小于4 ×10-5 。用这种方法不仅能够解决大体积的测量问题,还易于今后大体积复测。大体积经换算和修正后,结果如下:
V1=82.9075L u(V1) =2.1×10-4
V2=82.2713L u(V2) =2.1×10-4
为了验证体积比测量的准确性,也为了找出大体积可能的系统差,我们对目前常用的累积法做了改进。由于累积法每次测量耗时长,且前10次膨胀不计入,所以我们提出了增量法和预压累积法,分别对1∶100和1∶1000的体积比进行了复测,测量结果如表2 所示。
表2 不同测量方法得到的体积比
用增量法多次测量1∶100体积比,达到的相对标准差约为1 ×10-4 ;用预压累积法测量1∶1000体积比,达到的相对标准差约为6 ×10-4 。不同方法测得体积比结果的相对偏差为10-4量级,说明这几种测量方法是准确可靠的,也可以将增量法或预压累积法用于今后的体积比复现。
其它相关文章: