一种真空状态下的气体流量测量新方法

2012-04-23 董登峰北京航空航天大学仪器科学与光电工程学院

　　当空气绝对压力小于40 kPa 时, 目前尚无简便有效的气流质量流量测量手段, 为此本文设计了一套新颖的流量标定装置, 并提出一种了流量测量方法。在流量调节过程中, 调节阀必不可少。真空状态下, 流经调节阀的流量几乎完全由阀前、后压力、气流温度四个变量决定。本文由流量标定装置获取有效的数据样本, 基于多元非线性回归方法建立了流量与四者的关系表达式。一定范围内只要测定四个变量, 则能直接计算出相应流量。实验结果表明计算值与实测流量偏差小于3.0%。

　　真空气体流量的测量常见于需要真空气流的过程, 如宽范围湿度的发生过程, 卷烟的生产过程及大气环境的模拟过程等。在大气环境模拟过程中, 动态真空实验箱内真空环境的更新速度, 是衡量实验箱性能的一个重要指标。为控制动态真空实验箱内真空环境的更新速度, 必须实时测量真空状态下的气体流量。真空状态下, 气体流量的测量具有如下特点 :

　　(1) 流量密度小, 限制了涡街流量计与超声流量计的正常使用。对于前者相应的气流推力过小,对于后者则会产生阻抗匹配的困难。

　　(2) 不允许引入明显的压力损失。真空管道上安装流量计后增大了阻力, 产生较大的压损将使动力损耗大大增加, 不利于节能。因而孔板流量计、涡轮流量计、容积式流量计等均不适用。

　　(3) 流量计在负压管道上安装后, 如果存在泄漏很难觉察, 不仅会浪费动力, 而且会严重破坏内部气体环境。

　　综上虽然当前关于气体流量测量的方法多种多样, 但是基于这些方法设计的流量计一般仅针对非真空( > 100 kPa) 或真空度不高的情形。当气流绝对压力小于40 kPa 时, 当前市场上在售的流量计基本上都无法满足测量要求。在流量调节过程中, 调节阀必不可少。真空状态下, 气体通过调节阀的流量主要取决于四个因素, 阀前压力、阀后压力、流量系数、气流温度。利用调节阀的节流特点, 如果建立起流量与四者的关系模型, 调节阀本身即可以充当流量计, 那么通过测定上述四者的量值, 就可以间接确定真空状态下的流量。但在建立模型时由于真空状态( < 40 kPa) 下没有合适的流量计能够进行流量测量和标定, 所以无法确定流量值。为此本文基于动态平衡原理设计了一套新颖的流量标定系统,获取了可靠的数据样本; 然后利用多元非线性回归方法与Gauss-Newton 算法对数据进行建模, 确立了流量与四个变量的关系表达式; 基于此表达式只需测定四个变量便能直接计算出相应的流量。

1、调节阀的节流特性

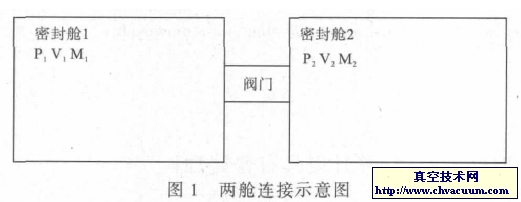
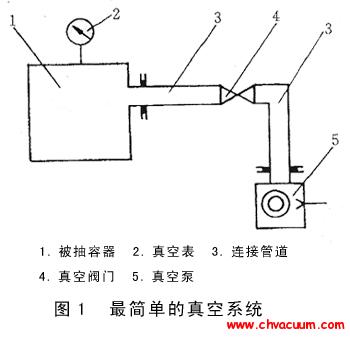
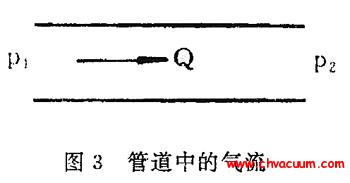
　　如图1 所示, 调节阀具有节流特性, 流经调节阀的流量可由式(1) 计算得到

　　式中,N为考虑到具体单位的数值常量;Kv为调节阀固有流量系数;p1为阀前压力,p2为阀后压力;X为压差比;M为气体的分子量;T为气流温度;Z为压缩因子,在真空状态下,其值接近为1;Fk为气体比热系数,对于空气Fk=1;Xt为临界压差比,主要取决于阀体的结构。对于可压缩流体的流动有阻塞流和非阻塞流两种情形,其判别标准为:若(p1-p2)/p1

　　从式(1)可知流量的大小主要取决于阀门与流体的物理特性,而且当阀门开度O发生变化时,Kv值也会相应改变。因而流量与阀门开度O、阀门上游压力p1、下游压力p2、气流温度T的综合函数关系可以表达为

　　由式(2)可知,如果能够获知流量与四个变量的关系模型,那么就可以通过测量四个变量计算出相应的实际流量。确定关系模型的首要前提是采取一定的方法获得有关流量与四个变量的有效数据样本。

2、基于动态平衡的流量标定方法

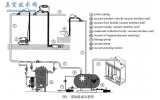
　　当绝压小于40 kPa时,目前没有合适的流量计直接进行空气流量标定,即式(2)中已知p1,p2,T,O无法测得准确的输出值Q,故难以对样本进行有效收集,为解决这一问题本文设计了一套流量标定系统,其结构如图2所示。利用该系统调节阀V1为任一开度时均能够实现对容腔C1、C2内真空气流压力的独立控制。当C1、C2内真空压力到达稳态,系统干路流量处处相等[5]。

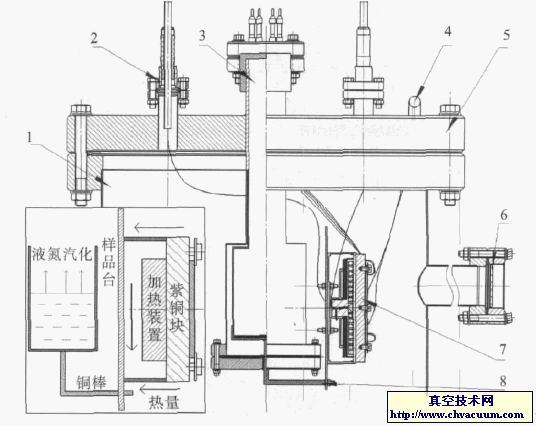
　　由图2知流量计安装在C0与C1之间。控制阀V0、V3安装在C1的上游,调节C1内的气流场压力;控制阀V2、V4安装在C2的下游,调节C2内的气流场压力;控制阀V1充当流量计,在一次流量测定过程中其开度保持不变。假定p0,p1,p2,p3分别为压力容腔C0,C1,C2,C3内的气流场压力。因p0为稳定的气源压力,其在实验过程中始终保持不变。考虑到p1,p2为真空,将p0设定约为100 kPa,从而满足常规流量计使用条件。当p0,p1,p2,p3均不再变化,整个系统进入动态平衡,流经V1与F1的流量相等,则流量计的读数即为气体流经调节阀V1的流量值。流量标定系统的实物装置如图3所示。