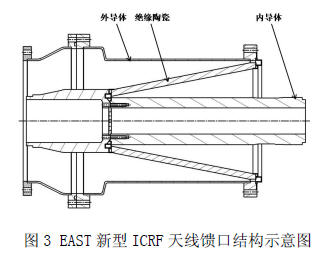
ESI离子阱质谱仪的三级梯度真空系统参数计算设计
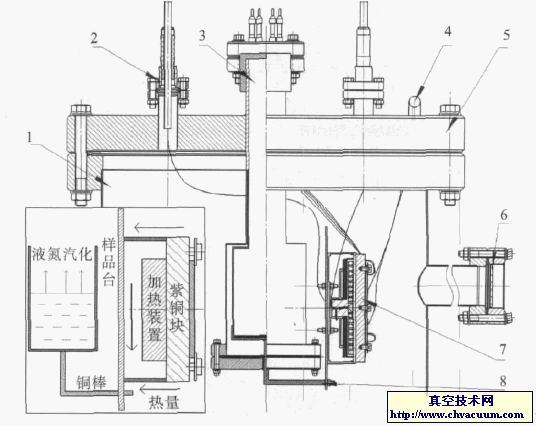
梯度抽气的作用是形成一个真空度逐步提高(压强逐渐减小)的工作环境。如前所述,三级真空度和泵的抽速已定。现在只能通过改变去溶毛细管、取样锥和离子透镜组的参数来最终取得所需的真空。
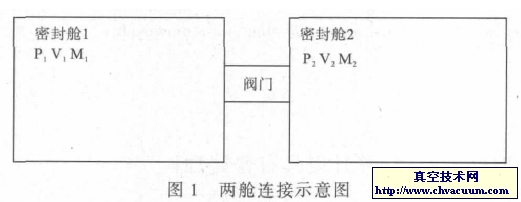
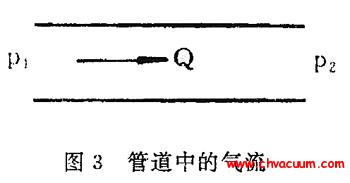
P2 = P1U/S (1)
式中U———管道流导
P1———前级真空腔(或大气)压力
P2———本级真空腔压力
S———本级泵的抽速
通过上式可以看出,只要求出各级真空腔的流导就可以计算出相应的真空腔压力。
去溶毛细管流导计算
抽气的最初阶段,气体的压力和流速较高,流动不稳定,气流漩涡时隐时现,这种状态称为湍流;随着压强降低,气流由湍流变成较规则的流动,从管道的中心到管壁各部分具有不同速度流层气体的粘滞力在流动中起主导作用,这种流态叫做粘滞流;介于这两种状态之间的叫湍-粘滞流(过渡流)。通常用雷诺数对它们加以区分。经计算,我们判断出去溶毛细管的流导可以采用湍—粘滞流长管流导的计算公式比较合理,由此推导公式如下:
U 为长管粘滞流流导,d 为长管的内径(cm),l 为管长(cm),P0 和P1 分别为大气和一级真空的压力。
取样锥流导计算
当气体流动进入高真空范围,气压进一步降低,气体分子平均自由程大于管道直径时,气体分子与管壁的碰撞为主,气体流动由各个分子的独立运动叠加而成,这种流动称为分子流;发生在中真空区域,介于粘滞流与分子流之间的流动状态叫做粘滞—分子流。这些变化和管道的尺寸、气体的性质及温度有关。为判断管道气体性质的变化,我们通常采用克努曾数判据,经计算得到流经取样锥的为粘滞-分子流(中间流)。取样锥的流导可以近似按孔的流导计算,孔的中间流流导只和面积成正比关系。取样锥的入口处于毛细管口后的超音速膨胀区,该处的压力远远大于一级真空腔内的平均压力,并且和真空腔内部去溶毛细管和取样锥的相对安装位置有很大关系。我们将取样锥入口的压力校正系数也一同考虑到取样锥流导的计算公式中,取样锥的流导的经验计算公式:
U = 11.6×A (3)
A 为孔的面积(cm2)。
离子透镜组流导计算
离子透镜可以近似看作为一个短管进行流导计算,按照上述的克努曾数判据计算,离子透镜的流导应当按照分子流计算:
U = 11.6×A×α (4)
A 为孔的面积(cm2),α 为由管长和管径确定的系数,其具体值可由表1 查出。由上述参数可以算出离子透镜中心孔的长度为11 mm,中心孔径的取值范围为1~4 mm 之间。
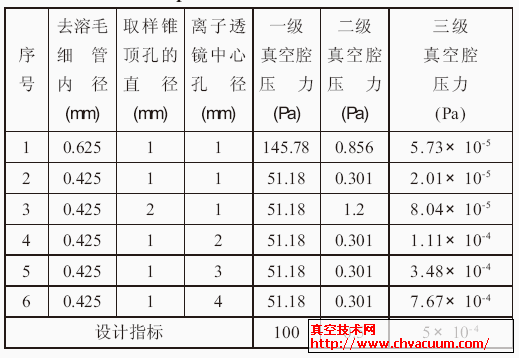
通过上面几个真空分隔部件的流导公式,再结合公式1,通过计算给出了不同设计参数的真空度计算结果,见表2。
通过表2 的计算数值和设计指标相比较,我们分别选用以下条件进行运算:内径0.425 mm和0.625 mm 的去溶毛细管,取样锥孔直径为1 mm和2mm,离子透阱中心孔径1mm、2mm、3mm、4mm。
表1 短管分子流流导的α 取值表
表2 不同参数时的真空度计算结果
结合工作压力应选择在低于极限压力半个到一个数量级的原则,最终确定去溶毛细管长度为180 mm,内径为0.425 mm。取样锥顶端的孔的直径为1 mm。离子透镜的中心孔径为2 mm。三级真空腔的理论真空度分别为51.18 Pa、0.301 Pa 和1.11×10- 4 Pa。最终实验验证三级真空的真空压力分别达到87 Pa、5.0×10- 1 Pa 和3.2×10- 4 Pa,这与理论计算值吻合的比较好,但均比理论值差一些,这是由于材料表面放气和结构漏气率所造成的。以上这些数据表明,通过理论计算对真空设计是有十分重要的指导作用的。
相关文章阅读: