煤气化核心调节阀的数值模拟与结构优化
该文以航天煤化工系统中的某型号笼式调节阀为研究对象,应用CFD数值模拟方法研究了调节阀的内流场特性。通过模拟给定压差下阀门不同开度的流量特性,得到调节阀的流量特性曲线,并与试验测定的数据进行比较分析,模拟值与试验值吻合较好。根据流场特性对流道做了优化并对新结构做了数值模拟,结果表明,优化后的流道流阻减小、涡流强度减弱、进而减少了能量损失。
引言
调节阀又称为控制阀,是过程控制系统中用动力操作去改变流体流量的装置,随着自动化程度的不断提高,调节阀已广泛地应用于冶金、电力、化工、石油等领域。在化工生产过程中,一个工艺过程的控制是否平稳,超调量、衰减比,扰动是否在规定的范围内,除了工艺设计合理、设备先进外,重要的一点就是调节阀能否按照主体控制意识准确动作,从而精确地改变物料或能量。如果调节阀的流量特性差、渗漏大、动作不可靠,就会使自动控制过程的质量变差,甚至失去调节作用,从而增加了劳动强度,给生产带来重大的经济损失。而航天煤化工系统中的主氧路氧气调节阀,系统对其调节的稳定性,可靠性及灵敏度有着更高的要求。因此,调节阀性能的提高对流程工艺效益的提高以及能源消耗的降低有着重要作用。近年来,随着计算流体动力学(简称CFD)软件的发展,通过CFD数值模拟来研究调节阀的流量特性并用来优化设计方案在阀门行业已开始应用。CFD技术在阀门设计中的应用使得阀门的结构设计更趋于合理,更有助于我国阀门行业开发新产品,加快缩小与国外差距的步伐。
1、调节阀的结构及流道模型的建立
文中以航天煤化工系统中的主氧路氧气调节阀为研究对象,其为笼式单座调节阀。该模型简化后的内部结构如图1所示,公称通径为80mm,总长为337mm。流体的流动方向为右进左出,通过调节阀芯的行程,来改变阀笼的流通面积,从而实现调节流量的目的。利用三维建模软件Solidworks,根据流道的几何尺寸以及阀芯与阀座的装配关系,对不同开度下的流体流道分别进行三维建模,为使流体流动更充分,阀前后流道均延长1000mm。图2所示为该调节阀流体流道的三维模型。
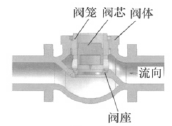
图1 调节阀内部结构图
图2 调节阀流道三维模型图
2、数学模型
2.1、控制方程
研究过程中合理假定调节阀内流体介质为不可压缩的黏性流体。无热能交换,不可压缩黏性流体控制方程由质量守恒方程(连续性方程)和动量守恒方程(N-S方程)组成,分别为:
质量守恒方程:
其中,u,v,w 分别是三个方向的速度矢量。
动量守恒方程(N-S 方程) :
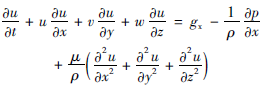 (2)
(2) 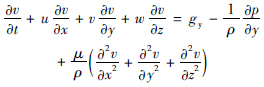 (3)
(3) 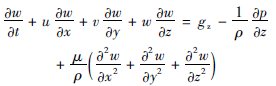 (4)
(4) 其中,p,ρ,μ分别是压力、密度、动力黏度。
2.2、标准k-ε模型
研究过程中湍流模型设定为工程中广泛使用的标准k-ε模型。
在标准k-ε模型中,紊流动能k方程和耗散ε方程分别为: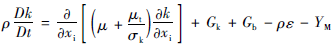 (5)
(5) 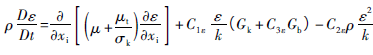 (6) 在上述方程中,Gk表示由于平均速度梯度引起的湍动能产生;Gb是用于浮力影响引起的湍动能产生;YM为可压速湍流脉动膨胀对总的耗散率的影响;湍流粘性系数
(6) 在上述方程中,Gk表示由于平均速度梯度引起的湍动能产生;Gb是用于浮力影响引起的湍动能产生;YM为可压速湍流脉动膨胀对总的耗散率的影响;湍流粘性系数 ![]() ;C1ε,C2ε为常数。
;C1ε,C2ε为常数。
3、数值模拟
将三维几何模型导入GAMBIT进行计算前的处理工作。确定了计算域之后,用GAMBIT对其进行非结构化网格划分,流道网格划分采用四面体网格,划分后网格数为100万左右。其中,调节阀开度为90%的流道网格划分如图3所示。

图3 调节阀开度90%时的流道网格划分示意图
选取该调节阀从10%~90% 到全开十个开度进行数值模拟。
将GAMBIT导出的网格文件读入FLUENT后,选择求解器,求解方程及模型(选用k-ε标准湍流模型),设置流体为水,设置进出口的边界条件分别为:入口压力p1=100kPa,出口压力p2=0kPa。进行流场初始化,设定控制参数及定义迭代次数后就可以进行求解。
4、结果分析
4.1、不同开度下流量特性模拟数据与液流试验台试验数据对比分析
流量特性是指介质流过阀门的相对流量与相对开度的关系。调节阀的流量特性是调节阀最重要的指标之一,在阀前后压差不变时得到的是理想流量特性。流量系数为Kv,定义为:
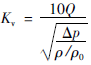 (7)
(7) 式中:Q为流量,m3/h;Δp为阀前后压差,kPa;ρ/ρ0为相对密度(规定范围内的水ρ/ρ0 =1)。
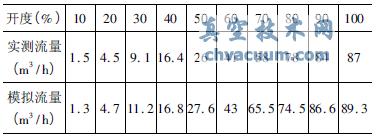
取阀前后压差为100kPa,由流量系数定义式可以推算出该压差下Kv=Q。将模拟所得的流量系数与通过液流试验台实际测量值进行对比(表1),并将两组数据进行拟合如图4所示。从图4可以看出,数值模拟曲线和实际测量值曲线基本吻合,趋势基本一致。通过比较,可以看出通过模拟所得的该调节阀的流量特性是可靠的,为调节阀的流道优化提供了依据。
表1 调节阀不同开度下流量模拟值与实测值数据表
据此,在产品方案的设计初期,可以运用数值模拟进行设计方案预选,进行调节阀从关闭到全开启范围的三维真实工作参数和介质的模拟,提供全面完整的流场信息,为改善阀门稳定性提供参考。后期待产品设计完成再辅以少量试验来校核确定方案,从而避免带有盲目性的大量试验。
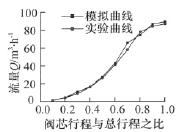
图4 调节阀流量特性模拟值与实测值对比曲线
运用CFD数值模拟方法进行产品研发设计,比以往设计过程(参见图5所示流程图) 更自由、更灵活,而且可以节约大量的人力和资金,大大提高研发设计效率。运用数值模拟方法还能对试验难以量测的量进行较为精确的估计,提供试验无法获得的数据,并能模拟较复杂或较理想的工况,拓宽试验研究的范围。
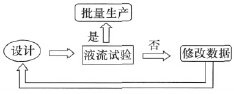
图5 调节阀传统设计过程流程图
4.2、不同开度下流场分析
由于该调节阀的固有流量特性为等百分比,主要工作区间为开度10%~90%,本文选取40%和90%两个典型开度进行重点分析。
在进出口压差为100kPa条件下,取该调节阀的全部流道和对称面进行分析,研究其内部的流场分布情况。
1)开度90%时流场分析
图6为对称面上压力云图,图7为对称面上速度矢量图。
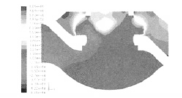
图6 调节阀开度90%时对称面上压力云图

图7 调节阀开度90%时对称面上速度矢量图
从图6可以看出,进、出口压力较为均匀,分别在100kPa和0左右,进出口压差较大,该压差主要用于克服调节阀流道内的阻力。在水流经过阀芯处有减压增速的效果。从图7中可以看出,进口流速比较均匀,出口流速分布不均匀。总体看没有很明显的涡流,只是在阀道左下部(见图7),有小部分涡动,可以考虑对此处流道进行优化。
2) 开度40%时流场分析
图8为调节阀开度40%时对称面上的压力云图,图9为开度40%时对称面上速度矢量图。

图8 调节阀开度40%时压力云图

图9 调节阀开度数0%时对称面上速度矢量图
从图8,图9可以看出,与90%开度时类似,40%开度下在水流经过阀芯处有减压增速效果,但90%开度时阀芯处水流速度的变化更加明显,高速流区域更大;相比90%开度时,在40%开度下,由于阀芯处过流面积较小,减压增速所涉及的流域小,因此速度强烈波动影响的范围相对较小,并且在出口处流速更趋于均匀。由于开度减小,进口和出口处的流速相对有所减小。
在40%开度下,在阀道左上部、右上部和右下部以及阀芯处有明显涡流出现。涡流的出现会消耗流体的能量,增大阻力系数。因此,要对出现涡流处的流道进行优化,以减少或进一步避免漩涡产生,减少能量损耗,提高流量系数。
5、调节阀流道改进优化
在阀门流道内产生的漩涡形成剧烈紊动的分离回流区是水头损失的主要原因。前文中对该阀体内流场数值模拟的结果表明该流道有待优化。流道中漩涡出现的部位需进行设计改进,使介质进入阀体后流线圆滑,并且在拐弯处适当减速,尽量避免折流。流道改进后的调节阀模型如图10所示。
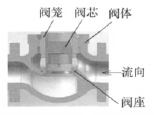
图10 流道改进后的调节阀模型
5.1 优化后不同开度下流量特性模拟数据与液流试验数据对比分析
仍以进出口压差为100kPa为条件,对改进后调节阀从10%~30%到全开等10个开度进行数值模拟,将模拟所得的流量系数与通过液流试验台实际测量值进行对比,如表2所示,将两组数据进行拟合如图11所示。从图11可以看出,数值模拟曲线和实际测量值曲线吻合较好。
表2 调节阀优化后不同开度下流量模拟值与实测值数据表
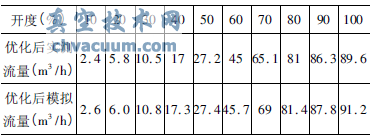
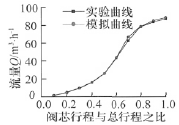
图11 优化后调节阀流量特性模拟值与实测值对比曲线
5.2 优化前后流场特性对比
图12所示为调节阀流道优化前后流量系数实测值对比,图13所示为40%开度下,优化后调节阀的对称面速度矢量图。
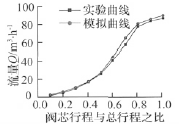
图12 流道优化前后实测值对比
由图12拟合曲线可以看出经优化后的调节阀流量系数有了提高。将图13与图9进行对比可以明显看出优化后流道左上部的涡流强度减弱了很多,流道右上部涡流也有减弱。但由于结构的限制,对该阀体流道没有做大的改动,后续可以设计流线型的阀体流道,从而使阀门的流阻更小。

图13 改进后调节阀开度40%时对称面速度矢量图
上述结果表明,增大阀门流动死角处的过渡圆角,可降低产生漩涡的可能性,并且能够使流场内的压力速度分布更趋于均匀,而且,阀芯处剧烈的减压增速区域明显后移,降低了流体对阀芯的冲蚀。可见,对阀门流道模型的数值模拟分析,可以方便地找出流道的不足之处并能有效的进行改进优化,使阀门的结构设计更趋于合理。
6、结论
(1)调节阀流量系数的模拟值和试验值吻合较好,表明CFD完全适用于调节阀的流场分析;
(2)通过数值模拟,得到了调节阀内部流体的流动情况: 速度场分布、压力场分布、流线走向、涡流等。调节阀传统设计理念是先初步设计出样品,通过5至6次的液流试验的结果,对阀门的结构尺寸进行反复修正,最终得出合理的阀门流量曲线,实现产品定型; 而基于CFD的调节阀辅助设计方法,改变了传统的调节阀设计理念,经过CFD优化后的产品只需通过1至2次液流试验作为对设计的验证,就能实现产品的定型,从而大幅度缩短设计周期,节省成本。综上所述,基于CFD的调节阀辅助设计方法,在突破国外产品在高压氧气调节阀的垄断方面,发挥了重要作用。
应用这种先进理念研发设计出的3″主氧路氧气调节阀已经在鲁西化工等煤化工生产线上使用,调节开度在30%-60% ,流量调节精确稳定,产品性能达到世界一流水平,能够完全替代进口产品,填补了当前国内氧路调节阀的空白。