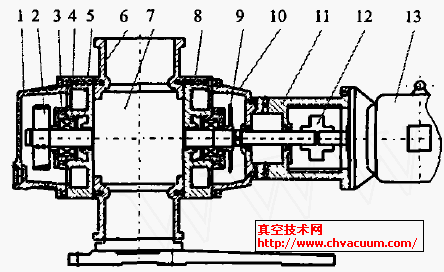
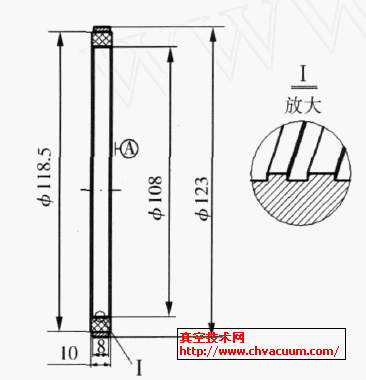
中小型引水式水电站调压阀尺寸优化

　　为保证工程安全并降低造价,中小型引水式水电站多采用调压阀作为调节保证措施,调压阀直径的确定不仅直接影响工程投资,且涉及到系统的平压效果。通过分析不同运行工况、水道系统最大压力上升值、机组转速上升率、事故甩负荷导叶关闭时间等多种因素对调压阀直径的影响,提出了合理的调压阀直径选取需满足的原则,并结合某电站调压阀直径的优化计算,验证了理论分析提出的原则。

　　在水电站运行过程中，为改善水锤现象，降低由机组突然甩负荷、水轮机导叶快速关闭带来的管道压力升高和转速上升值，通常会采取设置调压室的方式。但对一些中小型的长引水式电站，设置调压室可能受地形、地质等条件限制，同时需投入大量的人力和资金，因此需考虑其他调节保证措施来满足此类水电站的稳定运行。采用造价优廉的调压阀是中小型引水式电站中一种有效的调节保证措施。从20世纪80年代起，我国开始在长引水式电站中采用“以阀代井”的调节保证措施。湖南龙源电站是我国第一座采用调压阀代替调压井的试点电站，该电站压力引水管道总长1950m，设计水头83m，3台水轮机装设我国自行研制的TFW-400型调压阀。之后云南西洱河二级电站、贵州白水河一级电站、广西长滩河水电站等亦采用调压阀作为调节保证措施，有效降低了管道的压力升高值，确保了输水系统的安全，使电站运行稳定。但在以往的调压阀计算中，通常采用经验公式计算确定调压阀的直径，本文则通过水力过渡过程的计算，分析了调压阀的直径选取和优化问题，为中小型引水式水电站采用“以阀代井”的调保措施提供了理论依据与设计方法。

1、调压阀直径优化原理

　　调压阀的工作原理为调压阀与机组受同一调速器控制，在机组突甩负荷时，水轮机导叶快速关闭，同时调压阀开启，泄放机组由于导叶关闭而减少的过流量，待导叶完全关闭后，调压阀再以能保证允许管道压力上升值的速度缓慢关闭。调压阀启闭的非恒定流过渡过程可采用特征线法计算，其边界条件见图1。

图1 调压阀边界条件

　　调压阀进、出口断面C+、C-特征线相容性方程均成立，分别为：

　　其中

　　式中，Hp1、Hp2分别为调压阀进、出口断面的测压管水头;Cp、Bp、CM、BM为前一时刻t-Δt的已知量(t为时间，Δt为时间步长);Qp为调压阀的过流量;αp为调压阀的过流系数，表示不同开度下通过调压阀的单位流量;D为调压阀的直径;ΔHp为调压阀的水头损失。

　　将式(1)～(4)联立求解，可得：

　　将式(5)代入式(1)、(2)即可求出Hp1、Hp2的值。

　　由式(5)可知，调压阀在某一相对开度下的过流量为其直径的单调递增函数，说明调压阀直径越大，其过流量也越大。

　　当全部机组同时突甩负荷时，调压阀直径越大，可通过的过流量也越大，在机组导叶快速关闭、调压阀同时开启的过程中，机组转速和水道系统压力上升值越能得到好的控制。但在调压阀关闭过程中，过大的流量可能会造成管道压力出现新一波的上升，若第二波压力上升过大则可能超过允许的控制标准。图2为某电站调压阀直径分别为0.3、0.5m时全部机组甩负荷工况下的蜗壳压力变化过程线。由图可看出，相对于调压阀直径0.3m的情况，调压阀直径0.5m时第一波蜗壳压力并未上升，但由于调压阀直径过大，第二波压力远大于第一波，与上述分析一致。若要降低第二波的压力上升值，则需加长调压阀的关闭时间，而在更长的关闭时间中，更多的水流从调压阀流走，亦增加了系统的水能损失。

图2 某电站蜗壳压力变化过程线

　　当同一水力单元的部分机组突甩负荷时，若调压阀的直径过大，过多的流量将从调压阀流走，使受干扰的正常运行机组出力出现较大下降，由此可能发生相继甩负荷事故。

　　由以上分析可知，调压阀直径大小受运行工况、转速、水锤压力和造价等多方面因素的影响，因此选择调压阀直径时需综合考虑。调压阀直径的选取需满足以下两点原则：①最小的调压阀直径应保证机组快速关闭时转速上升率和第一波水锤压力满足调保要求;②最大的调压阀直径应满足调压阀全开时的流量与机组额定流量基本相同，同时保证调压阀关闭时产生的第二波水锤压力亦满足调保要求。

2、算例分析

　　某引水式水电站有压力输水系统，采用“一洞两机”的布置方式，装机容量为2×2.1MW，额定水头123.4m，压力管道直径1.8m，装设两台水轮机，水轮机的额定流量为1.966m3/s，额定出力为2.21MW，额定转速为1000r/min。由于该电站引水道较长、流量较小，且投资较少，因此拟采用调压阀作为调节保证措施。电站输水系统布置见图3，总引水道长约4100m，每台机组设置一个调压阀。

图3 电站输水系统布置简图(单位：m)

　　根据相关规范选取本电站的调保计算控制标准为机组最大转速升高率≤50%，设置调压阀时蜗壳最大压力升高率一般取为0.15～0.20，在该电站计算中，取调压阀正常工作时蜗壳最大压力升高率为0.175，即蜗壳最大压力控制值为153.509m。

2.1、全部机组甩负荷工况

　　选取出现蜗壳最大压力的工况(最大水头下两台机同时突甩负荷，机组导叶正常关闭)为工况1，在工况1下取调压阀直径分别为0.2、0.3、0.4、0.5m进行计算，得到相应的蜗壳末端压力、机组转速上升率及机组和调压阀的流量变化。机组—调压阀联动的启闭规律选为：机组导叶以15s一段直线规律关闭，同时调压阀以15s一段直线规律开启，达到全开并滞后10s后，调压阀再以180s一段直线规律关闭。表1为不同调压阀直径时的蜗壳末端最大压力、机组最大转速上升率、机组最大引用流量和调压阀最大泄流量，图4为不同调压阀直径下蜗壳末端压力变化过程线。

表1 工况1下不同调压阀直径计算结果

　　由表1、图4可看出：①调压阀直径为0.2m时，由于调压阀直径过小，导致调压阀泄流能力不足，并未起到很好的降压效果，在机组导叶关闭结束时刻，蜗壳末端出现最大压力为171.06m，超过调保控制标准，机组转速上升率也较大。②调压阀直径为0.5m时，机组转速上升得到了很好的控制，同时蜗壳末端压力在机组导叶关闭过程中几乎未上升，反而有很大的下降，最初的降压效果很好，但由于调压阀直径过大，导致系统总流量增加过大，单个调压阀最大泄流量达4.072m3/s，在调压阀关闭结束时刻，蜗壳末端新一波的压力上升到最大，远超过了第一波的最大压力，超出了调保控制标准。③调压阀直径为0.3m时，机组导叶关闭过程中系统总流量基本保持不变，蜗壳压力上升较小，且调压阀关闭过程中蜗壳压力变化很小，蜗壳压力变化过程线围绕初始压力小幅度震荡，第二波水锤压力与第一波基本一致。④调压阀直径为0.4m时，机组转速上升率较低，虽第二波压力超过第一波，但蜗壳末端最大压力仍控制在允许范围内。因此，从全部机组甩负荷工况结果看，调压阀直径为0.3、0.4m时，机组转速和水锤压力均能得到控制。

图4 不同调压阀直径时蜗壳末端最大压力、机组相对转速和系统总流量变化过程线

2.2、单台机组甩负荷工况

　　选取1台机组突然甩负荷的工况为工况2，在工况2下取调压阀直径分别为0.2、0.3、0.4、0.5m进行水力干扰计算，得到不同调压阀直径下机组的力矩变化情况，分别见表2、图5。机组—调压阀启闭规律同全部机组甩负荷工况。

表2　工况2下不同调压阀直径计算结果

图5 不同调压阀直径时正常工作机组相对力矩变化过程线

　　由表2、图5可看出：①调压阀直径为0.2m时，调压阀直径较小，致使正常工作机组的力矩上升较大，最大力矩上升率达19.0%。②调压阀直径为0.4、0.5m时，由于调压阀直径过大，在甩负荷机组导叶关闭、调压阀开启过程中大部分水流从该调压阀流走，正常工作的机组受到了较大的扰动，出现较大的力矩下降(最大力矩下降率分别达20.5%、44.8%)。因此，选择直径为0.3m的调压阀较为合适。

　　通过上述两个工况的计算分析表明，该电站选用直径为0.3m的调压阀作为调节保证措施最为合适，这样可在机组导叶快速关闭时，保证机组转速上升和压力上升均满足调节保证要求。

3、结语

　　分析了影响调压阀直径大小的多种因素，提出了合理的调压阀直径需满足的两个原则，确保了调压阀关闭时产生的第二波水锤压力亦满足调保要求。并结合某电站调压阀直径的优化计算，验证了理论分析提出的原则。该原则同样适用于任何采用调压阀作为调节保证措施的中小型引水式电站，可供调压阀直径的优化设计参考。