基于矢量控制原理的电动执行机构

　　为了实现电动执行器在精确性、灵敏度、快速反应和稳定性等方面，将基于矢量控制策略应用于电动执行机构。采用矢量控制方法，可实现优良的控制品质。并根据矢量控制理论设计出的新型电动行机构，仿真和实践结果表明：具有良好的动静态特性。

1、引言

　　电动执行机构在控制系统中又称为终端控制元件，是自动控制系统中不可缺少的重要组成部分。它是利用电源为动力并在某种控制信号作用下工作，能提供直线或旋转运动的驱动装置。

2、矢量控制策略

2.1、矢量控制理论的提出和坐标变换

　　矢量控制在国际上一般多称为磁场定向控制(FieldOrientation)，亦即把磁场矢量的方向作为坐标轴的基准方向，电动机电流矢量的大小、方向均用瞬时值来表示。1971年，由德国西门子公司的Blaschke等人将这种一般化的概念形成系统的交流电动机的矢量控制(TransvectorContrl)理论，从理论上解决了交流电动机转矩的高性能控制问题。矢量控制理论的基本思想是在三相交流电动机上模拟直流电动机转矩控制的规律。通常在磁场定向坐标上，三相绕组在空间位置上互差3π/2rad机械角度，设在三相绕组中通以三相对称电流，在相位上互差3π/2rad电角度，产生的合成磁场具有以下特点：

　　(1)随着时间的推移，合成磁场的轴线在旋转，电流交变一个周期，磁场也将旋转一周;

　　(2)在旋转过程中，合成磁场强度不变，故称圆形旋转磁场。

　　考虑两相对称绕组，其在空间位置上互相“垂直”，互差3π/2rad电角度;两相交变电流在相位上互差3π/2rad电角度。将两相对称电流通入两相对称绕组，产生的合成磁场将具有与三相旋转磁场同样的特性。如果在旋转体R上放置2个匝数相等、互相垂直的直线绕组M和T，如图1所示。

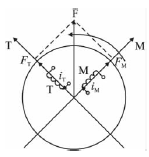
图1 两相直流旋转绕组示意图

　　则当2个绕组内分别通入直流电流iM和iT时，它们的合成磁场仍然是恒定磁场。如果调节任何一个直流电流(iM或iT)，则合成磁场的磁场强度也得到了调整。当R旋转时，两绕组同时以同步转速旋转，合成磁动势产生的合成磁通也会旋转，此恒定磁场将子空间形成一个机械旋转磁场，它与前面介绍的三相、两相绕组产生的磁场完全可以等效。当观察者站到铁心上和绕组一起旋转时，看到的将是2个通以直流的、相互垂直的固定绕组。如果采取补偿措施补偿掉绕组T产生的磁动势FT，电动机的主磁通只由M绕组产生，并和iM成正比。而T绕组中电流iT和磁场Φ作用将产生旋转，其大小只与电流iT成正比，这与直流电动机转矩产生的原理非常相似，得到在静动态性能上完全能够与直流调速系统相媲美的交流调速系统。因此，必须对电动机的参考坐标系进行变换。

2.2、矢量控制的实现

　　在研究矢量控制时，定义有三种坐标系统，即从三相到两相的静止坐标变换(3s/2s变换)和从两相静止到两相旋转地坐标变换(2s/2r变换)。

　　一个旋转矢量i从三相定子A-B-C坐标系变换到两相定子α-β坐标系，称为Clarke变换，也叫作3s/2s变换，其矩阵形式为式(1)：

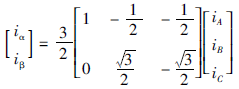
　　其原理示意图如图2所示。

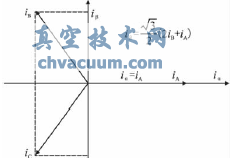
图2 CLARKE变换示意图

　　其逆变换，即Clarke逆变换或2/3变换矩阵式为式(2)：

　　一个旋转矢量i从d-q垂直坐标系变换到M-T定向坐标系，称为Park变换，也叫作交/直变换，其矩阵形式为式(3)：

　　其变换原理图如图3所示。

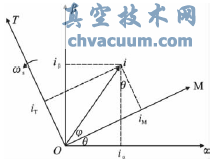
图3 PARK变换示意图

　　其逆变换，即Park逆变换或直/交变换的矩阵形式为式(4)：

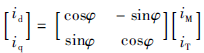
3、系统的基本方程式和结构框图

　　下面给出异步电动机两相以同步速旋转，按转子磁场定向的M、T坐标的数学模型。

　　(1)电压方程

　　(2)磁链方程

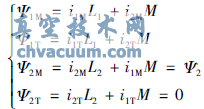
　　(4)电磁转矩方程

　　以上各式中，r1、r2为定转子电阻;L1、L2为定转子自感;M为定转子互感;u1M、u1T、u2M、u2T为M、T轴定转子电压;ωs为转差角频率;ω1为同步旋转角频率;T为电磁转矩;i1M、i1T、i2M、i2T为M、T轴定转子电流;PN为电动机极对数;Ψ1M、Ψ1T、Ψ2M、Ψ2T为M、T轴定转子磁链;P为微分算子;Ψ2为转子磁链。

　　交流异步电动机变频调速矢量控制系统的结构框图如图4所示。图中有上标的控制量为指令值，其余为实际值。首先将角速度指令ω*和ω的偏差信号e送入速度调节器，其输出即为T*指令。由上面的矢量控制基本方程式可求出T*、i*1M、i*1T、Ψ2、ωs。经过一系列坐标变换后，即可得到三相电流指令I*a、I*b、I*c。在电流调节部分，由电流指令和经霍尔式电流传感器检测出实时电流相比较的偏差送入电流调节器。将输出信号送给IGBT逆变器达到变频调速的目的。

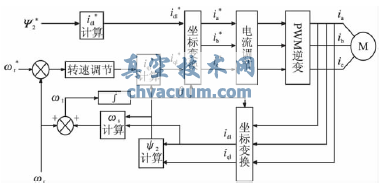
图4 变频调速矢量控制系统的结构框图

4、基于MATLAB的变频调速矢量控制的仿真

　　由上节推导的矢量控制系统的基本方程式，以及交流异步电动机变频调速矢量控制系统的结构框图，可得出在Simulink中的仿真结构图，如图5所示。

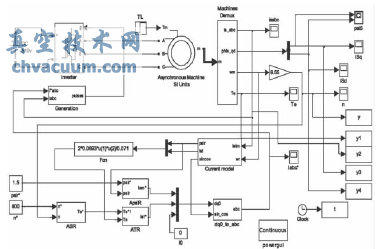
图5 Simulink中的仿真结构图

　　在Simulink的仿真结构图中，系统速度调节器(ASR)的输出信号是转矩给定T*e。其内部构造为如图6所示。其中转矩限幅设为300，Kp设为12，Ki设为24。

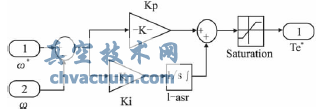
图6 系统速度调节器子模块

　　电流调节器(ACR)实现实际电流随给定电流的变化，采用电流滞环控制原理来实现电流的调节。以A相为例，控制原理如图7。将给定电流i*a与输出电流ia进行比较，电流偏差△ia超过±h时，经滞环控制器HBC控制逆变器A相上(或下)桥臂的功率器件动作。B、C二相的原理图均与此相同。

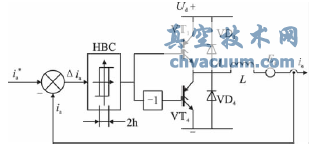
图7 电流滞环控制的A相原理图

　　其内部构造如图8所示。

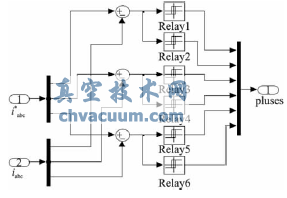
图8 系统电流调节器子模块

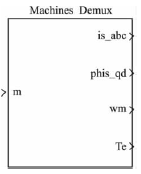
图9 电机测试信号分配器

　　滞环宽度设为20。

　　在仿真过程中用到的电机测试信号分配器(Ma-chinesMeasurementDemux)，如图9。在仿真过程中，选择电动机转速、电动机机械转矩、三相定子电流和同步d-q坐标下的q轴下的定子磁通和d轴下的定子磁通为输出信号。

　　异步电机参数：采用鼠笼式异步电动机，线电压380V;额定频率50Hz;定子内阻0.435Ω;定子漏感0.004mH;转子内阻0.816Ω;转子漏感0.004mH;互感34.7mH;极对数为4。仿真方法选择为固定步长(fixed-step)。仿真时间设为0～1s。得到的电动机转速、电动机机械转矩、三相定子电流和同步d-q坐标下的q轴下的定子磁通和d轴下的定子磁通的响应曲线如图10～14所示。

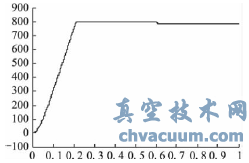
图10 电动机转速响应曲线

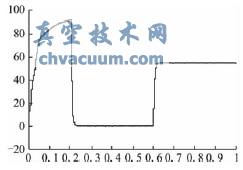
图11 电动机机械转矩响应曲线

图12 三相定子电流曲线图

图13 q轴下的定子磁通响应曲线

图14 d轴下的定子磁通响应曲线

4、结束语

　　本文从矢量控制的基本原理、异步电机的数学模型以及利用Matlab/Simulink工具出发，构造了矢量控制系统的仿真模型并仿真结果进行研究。研究结果表明，按转子磁链定向的异步电动机矢量控制系统具有动态性能好、调速范围宽的优点，且由以上实验结果表明，仿真实现的矢量控制算法，在异步交流电机驱动的应用上，无论是控制电机的速度，还是控制位置，效果都很理想。