基于遗传算法的最小流量阀自适应控制器的研究

　　目前很多最小流量阀的控制系统是非线性、有时滞且存在时变，虽然静态时控制系统经整定后是稳定的，但热态实际运行时，常常会出现振荡。本文提出了遗传算法优化自适应控制器的方法，与响应曲线法和Ziegler-Nichols法得到的PID参数仿真比较表明，遗传算法优化的自适应控制器应用于最小流量阀控制器参数优化是可行和有效的。

一、引言

　　最小流量阀安装于给水泵和除氧器或冷凝器之间，由于最小流量阀执行器的气缸容积大，所以该系统是非线性、时滞且存在时变，研究者无法建立精确的数学模型，常常需要经过大量的尝试才能得到相关的PID控制参数。

　　本文提出一种基于遗传算法自适应PID控制器，通过分析热态的真实参数解析一个确保稳定的PID参数，再利用遗传算法在临域搜索到一组自适应时变后的最优PID参数，让系统始终处于稳定状态。该算法可以较高效地找出符合设计要求的一组调节参数，系统具有响应快，稳定性优等特点。

二、最小流量阀时变系统

　　最小流量阀慢时变系统主要由控制器、增压器、切换阀、快速排气阀和气缸等组成。实际运行时，由于工况的变化以及该阀的执行器容积大，该系统是滞后、时变的系统，传统的PID控制器策略，常常导致系统波动或振荡。

三、基于遗传算法自适应控制器

　　遗传算法自适应控制器原理框图如图1所示，由参数辨别机构、控制器解析器、遗传算法、控制参数设定和自适应PID控制器等组成。

　　首先通过参数辨别机构设别被控对象的参数，得到一个近似的对象模型，按给定的性能指标根据控制器的方法解析出控制器初始运行时一组PID参数，保证系统初次运行时是稳定的。热态运行时，参数辨别机构首先识别对象的模型参数和各项性能指标是否满足用户需求，如不满足，用解析法求得一组自适应控制器PID参数最优解或次最优解，依据该组参数确定遗传算法的搜索范围，并运行遗传算法程序，得到新的一组PID参数，通过控制参数设定机构更新控制器的PID参数再次运行。整个程序的固定更新周期是600s，K1和K2是否闭合，是否进行遗传算法的参数整定，取决于参数性能指标是否满足工艺的要求，因此，该控制器具有自适应的功能，能及时调整控制器的参数，克服干扰，确保系统始终是稳定的。

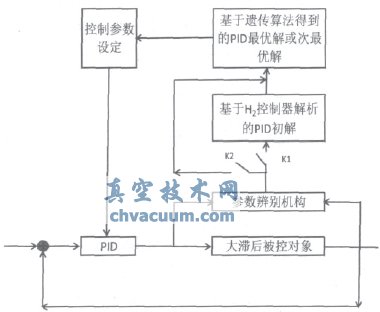
图1 遗传算法自适应控制器原理框图

四、控制器参数解析法

　　最优控制理论的出发点是使某一已知输入产生的平方误差积分最小化，等价地最小化加权灵敏度的2范数：Min2

　　假设设计对象：依据控制器的优化性能指标得到的单位反馈回路控制器为：C= =

　　与PID控制器C=Kc(1++TDS)。比较得到的PID如下：

P= I=+ D=

五、遗传算法控制器的参数整定

　　5.1、遗传算法流程图

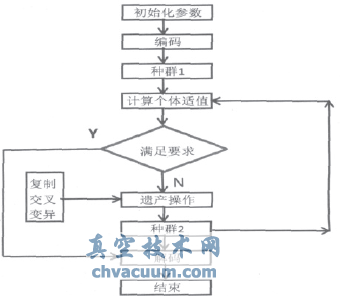
图2 遗传算法流程图

　　5.2、参数编码

　　把一个问题的可行解从其解空间转换到遗传算法所能处理的搜索空间的转换方法称为编码。编码方法主要有实数编码方法、二进制编码方法、浮点数编码方法等等。本文采用的是实数编码方法。

　　5.3、确定适应度函数。

　　衡量一个控制系统的指标有三个方面，即稳定性、准确性和快速性，因此，参数选择的最优指标：J=其中，e(t)为系统误差，u(t)为控制器输出，为上升时间，、、是权值。取适应度函数为：F=1/(J+0.0001)。0.0001是防止无穷大，导致无意义。这样当找到最大适合度的解，也就找到最小目标函数的解，寻优成功。为了避免超调，采用了惩罚功能，即一旦产生超调，将超调作为最优指标的一项，此时最优指标：如果e(t)<0，则J=式中为权值，且》。

　　5.4、选择控制参数。

　　遗传算法控制参数包括群体规模N，交叉概率Pc和变异概率Pm。这些参数的选取对遗传算法的搜索效率和寻优的最终结果有很大影响。这里取N=30，Pc=0.89，Pm=0.032。

　　5.5、初始群体形成。

　　为了防止参数范围过大，依据解析法计算出Kp、Ki、Kd三个参数值，然后利用这组参数确定遗传算法优化区域，这样有利于缩小搜索域，减少寻优的盲目性，降低计算量，迅速找到最优解的位置。本文先设定30个初始种群。

　　5.6、遗传操作。

　　遗传算法的基本操作是复制、交叉和变异。这里复制采用的是适应度比例法，交叉使用单点交叉和均匀变异的算法。

　　5.7、评价与判定。

　　计算新群体的适应值，然后判断是否满足终止条件-收敛于一个值J已达最小或已达到预定的指标，如果满足，结束遗传算法迭代;如果不满足则返回重新进行遗传操作。

六、系统仿真结果比较

　　6.1、参数辨别后被控制对象为一阶惯性纯滞后对象，其传递函数为：

　　6.2、采用响应曲线法整定PID的方法得到的控制器及参数是：Kc=1.4，Ki=0.008537，Kd=58.8。

　　6.3、采用ZN法整定PID的方法得到的控制器及参数是：Kc=1.3680，Ki=0.0096，Kd=50.8110，响应曲线法和ZN法的单位阶跃响应，仿真如图所示：

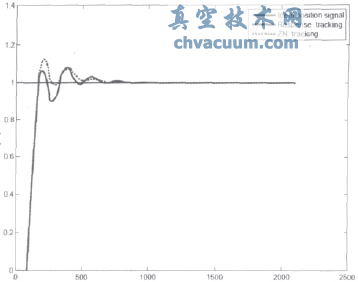
图3 响应曲线法和ZN法的阶跃响应图

　　6.4、先用法解析法得到初始控制器的PID参数为：Kc=0.788，Ki=0.008565，Kd=0.1726，再利用遗传算法在其临域搜索得到的控制器PID参数是：Kc=2.3512，Ki=0.4630，Kd=0.0161，解析法和遗传算法优化得到的PID参数输出响应，如下图所示：

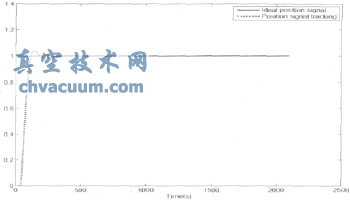
图4 遗传算法优化得到的PID参数输出响应图

　　6.5、即使工况变化后，仿真表明，遗传算法的方法得到的PID控制器，在超调量、上升时间等主要的控制系统的性能指标上均优于响应曲线法和ZN法，具有良好的动静态特性。

七、小结

　　本文提出了基于遗传算法的自适应控制器，解决了最小流量阀大滞后时变控制系统的不稳定振荡的问题。通过与一般响应法自整定和ZN法系统仿真比较，遗传算法优化后的自适应控制器具有更好的鲁棒性和准确性，是一种具有较好实用性、值得推广的PID参数优化控制器。