调节阀振动对阀内流场影响的数值模拟

　　调节阀振动问题在高参数汽轮机中普遍存在，已严重影响到机组运行的经济性和安全性。调节阀振动为复杂的流固耦合，依靠数值模拟揭示由流体诱发振动的原因逐渐成为重要的手段，但是目前针对调节阀的大部分数值模拟并未考虑阀杆系统振动对阀内流场的影响。

　　调节阀振动问题在高参数汽轮机中普遍存在，已严重影响到机组运行的经济性和安全性。调节阀振动为复杂的流固耦合，依靠数值模拟揭示由流体诱发振动的原因逐渐成为重要的手段，但是目前针对调节阀的大部分数值模拟并未考虑阀杆系统振动对阀内流场的影响。该文在数值模拟中利用Fluent中动网格模块和UDF函数，对比分析了阀碟在静止和不同振幅、振动频率下对阀内流场的影响。在网格变形中使用了一种新颖的网格控制方法，即固定阀碟边界层网格使网格在较大尺度区域变形，确保了数值计算准确、顺利的进行。数值计算结果表明当阀碟顶端振幅小于0.6mm时，阀碟上压力呈现随机波动;当阀碟顶端振幅为1mm时，阀碟上压力随阀碟移动出现明显的周期性波动，此时数值模拟应考虑阀杆系统振动的影响。随着振动频率的增加，阀碟上周期性的压力波动逐渐滞后于阀碟移动，当频率达到193.6Hz时周期性波动消失。

　　调节阀位于主蒸汽管道和汽轮机之间，是控制机组功率的重要通流部件。随着机组单机容量增加和蒸汽参数的提高，汽轮机调节阀常处于极其严酷的工况环境中，由流体诱发调节阀的振动所产生的事故屡见不鲜，已成为威胁电厂安全运行的重要因素。随着CFD的不断发展和完善，数值计算因其方便性和可视化等优点受到了众多学者青睐，在分析流体诱发的调节阀振动中扮演越来越重要的角色。但真空技术网(http://www.chvacuum.com/)认为由于调节阀振动是一种复杂的三维流固耦合现象，到目前为止对于该问题的机理始终没有明确的论断。

　　Araki认为当调节阀中阀杆系统的振动在小开度时为一阶纵向高频振动，在开度逐渐增大后主要为一阶弯曲振动。Zhang通过二维定常数值模拟指出阀内不对称流是引起振动的主因。Morita的三维非定常数值模拟进一步表明阀碟下方高压区的周向移动导致了阀杆系统的振动。Morita还通过实验研究了阀杆在弱连接下的压力波动和振动的关系，指出在中等升程时压力波动和阀固有频率之间存在锁定现象，在锁定区域阻尼比接近于零且振幅较大，而在非锁定区域阻尼比大于5%。Tecza通过有限元法确定了阀杆系统的固有频率，并指出阀碟最有可能的运动为倾斜和摆动，并按照阀杆摆动频率550Hz最大摆动角度为±0.02°进行了瞬态力响应分析。Yonezawa的研究表明阀碟在灵活状态下的压力波动高于阀碟紧固时的波动，将阀杆系统的振动分为振动幅值较小时的强迫振动和振动幅值较大时的自激振动。国内关于调节阀的数值计算研究往往不考虑阀杆系统振动的影响，用数值模拟分析调节阀的阀型对振动、流量、压损、流型等因素的影响，而在调节阀快关和开启特性中不得不考虑阀碟移动，利用动网格计算阀内的瞬时流场的变化。但是在计算过程中由于网格畸变过大而导致计算发散一直是困扰数值计算能否顺利进行的关键因素。通过增加网格尺度减小网格畸变往往收效甚微，甚至有时还会因网格尺度过大而影响计算准确性。

　　从这些研究可以看出，以往借助CFD分析阀内的流型及流体诱发的调节阀阀杆系统振动大都忽略振动对阀内流场的影响。但当振动幅值较大时，必然会对内部流场的产生影响。本文针对以上问题，利用Fluent中的弹簧光顺模型和UDF函数，对比分析了某600MW模化调节阀的阀碟顶端振幅分别为0.6mm、1mm，及振动频率分别为46.4、92.8、185.6Hz时阀杆系统振动对阀内流场的影响。计算中提出的保护边界层的网格变化方法和数值计算结果为后续数值计算中网格控制和是否考虑阀杆系统振动对阀内流场的影响提供了重要的参考。

1、数值计算的物理模型

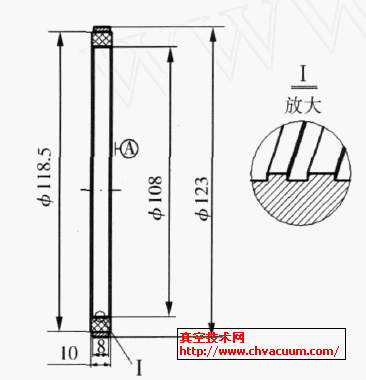
　　根据相似原理对某电厂600MW调节阀进行了模化实验，图1为模化后调节阀沿进口方向中心截面示意图。阀杆和阀碟所组成的系统可看做为以提升机构与阀杆连接处为固定点，顶端带有集中质量的长细粱结构[3]。由于调节阀在中等升程下，阀碟上压力波动呈现以低频占优的宽频激励特性，所以主要考虑阀杆阀碟所组成系统的一阶弯曲模态对阀内流场的影响。利用Workbench计算此调节阀阀杆系统固有频率，结果表明此调节阀阀杆系统一阶弯矩的固有频率为46.4Hz。为对比阀杆系统按照一阶弯矩振动在不同振动频率下对阀内流场的影响，计算了频率分别为一阶弯矩频率及2倍、4倍一阶弯矩频率(即频率分别为：46.4、92.8和185.6Hz)这3种方案。为对比不同幅值对阀内流场的影响，计算了阀碟固定、阀碟顶端振动幅值为0.6和1mm这3种方案。以上计算中，阀杆系统振动方向为沿图1中进口中心截面。为后续分析方便，定义三维坐标所指方向如下：x轴正方向所指的沿来流方向为东侧用E表示，x轴负方向所指为西侧用W表示;y轴所指方向沿阀杆轴向;z轴所指方向垂直于沿来流中心截面，如图1、2所示。

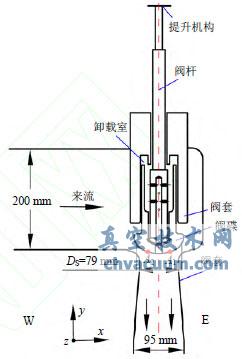
图1 调节阀结构图

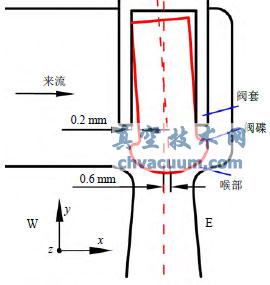
图2 阀碟偏向西侧示意图(h=0.6mm)

　　图2为阀碟顶端最大振幅h=0.6mm时的阀碟偏向东侧示意图，可以看出阀碟可能出现的最大振幅主要由阀碟和阀碟套间隙0.2mm决定。随着使用时间增加，阀碟表面的涂层不断脱落此间隙可达到0.4mm，此时阀碟顶端振幅为h=1mm。由于卸载室内流过的流量占主流流量小于1%，对主流的影响可忽略不计，因此在动网格计算中不考虑由卸载室流过的流体。

2、数值计算方法和动网格设置

　　本文湍流模型采用Fluent中基于realizablek-ε的两方程的DES模型。DES方法结合了雷诺平均与大涡模拟技术的优点，在近壁面的附面层内采用RANS方法，用realizablek-ε两方程模型模拟其中的小尺度脉动运动;在远离物面区域将湍流模型耗散项中的湍流尺度参数用网格尺度与一常数的乘积代替，使其起Smagorinski大涡模拟的亚格子雷诺应力模型的作用。这样既能在附面层内发挥前者计算量小的优点，又可以在远离物面的区域对大尺度分离湍流流动进行较好的模拟。

　　选取实际运行和模化实验中阀杆系统振动较大的工况，即相对升程(调节阀的绝对升程与配合直径比值)εL=11%，压比(调节阀出口静压与进口总压的比值)ψP=0.8作为计算工况。进口设为总压P0=123.5kPa，温度为298K。出口设为静压，其值P2=98.8kPa，温度为295K，所选取数据均为模化实验所测。

　　结合Fluent中UDF函数和弹簧光顺模型可实现阀碟在东西截面上以不同振幅和频率按正弦振动。UDF函数中主要通过式(1)控制振动。

cg_omega=Acos(BTime) (1)

　　式中：cg_omega为在xy平面内转动角速度，参数B控制频率，A控制振动幅值。Fluent中弹簧光顺法把网格的边理想化为节点间相互连接的弹簧，网格移动前弹簧组成的系统处于平衡状态。在网格边界节点发生位移后，会产生与位移成比例的力，从而由力转化出网格节点移动的距离。弹簧光顺方法并不将网格质量作为网格更新的判断因素，而只是单纯的将边界运动作为参数扩散至计算域中，因此无需插值，网格拓扑始终不变。

　　网格在ICEM中生成且全都为六面体结构化网格，总体网格数为800万。网格未发生移动时，在ICEM中网格质量2项评价标准如下：Determinant2´2´2>0.6，网格角度Angle>18°。使用Fluent计算时，当网格质量Determinant2´2´2>0.2且网格角度Angle>9°就可以确保数值计算顺利进行，由此可见初始时网格质量非常高。为保证阀出口为均匀流和避免回流的产生，将阀出口加长到出口直径的10倍，加密了喉部和阀碟下方流动变化较为剧烈的区域网格，保证在此区域内网格均匀变化和边界层内y+<=5。

　　图3为沿东西方向中心截面网格和网格变形后的局部示意图。由图3可以看出，在阀座喉部区域网格很密，阀碟周围第一层网格厚度为0.004mm。若不加以特殊处理，阀碟移动极易使边界层网格畸变过大而使计算发散。考虑到边界层内流动对流场的巨大影响，同时为保护阀碟处边界层网格，将包围阀碟部分区域网格设置为刚体区，即在计算中这部分网格不会变形。而此区域外的网格设置为变形区，即在阀碟移动中这部分网格会产生相应的变形，刚体区域和变形区域的划分如图3所示。通过控制弹簧光顺法中两个参数：弹簧常数因子与边界节点松弛因子，将网格中较大的变形控制在变形区域中靠近刚体区外围，而保证靠近阀座处较密的网格基本不变。由图3可以看出，当阀碟顶端偏向东侧1mm后喉部网格并没有发生畸变。将阀碟顶端偏向东侧1mm的网格重新导入ICEM中，其网格质量为：Determinant2´2´2>0.25，网格角度Angle>10°，足以满足Fluent计算中对网格的要求动网格常用于调节阀在开启或关闭计算中，此时由于阀碟位移较大使得网格变形量增大，为保证网格在大变形后畸变率低不得已采取较粗的网格，边界层网格通常难以严格满足湍流模型的需求。在中小升程下调节阀内流动往往为复杂的三维超音速流动，粗网格通常难以精确的捕捉激波、射流分离和边界层内的诸多流动细节，因此所得的结果往往只能定性的分析阀内的流动情况。本文在数值计算中所采用DES湍流模型虽对流过复杂机构的高雷诺数分离流具有非常高的预测能力，但是DES湍流模型高度的依赖网格尺度、网格质量和边界层内的网格布置。针对阀碟小幅振动特性，借助Fluent中弹簧光顺模型，创新性的将边界层网格刚体化，将阀碟移动造成的网格变形“转移”到相对尺寸较大的区域，既实现了800万结构网格网格变形也满足了湍流模型对网格的需求。

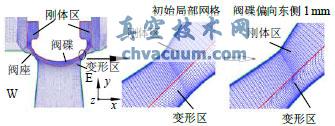
图3 沿东西方向中心截面初始网格和局部网格变形图

3、数值计算结果

　　在阀碟下表面沿振动的方向上设置了两个监测点A1和A2，其位置如图1中所示。图4为阀碟静止状态下，阀碟上两测点随时间的压力变化时域图，可以看出两测点处的压力呈现无规则的波动状态。图5和图6是阀杆系统以频率f=46.4Hz振动阀碟顶端振幅分别为h=0.6mm和h=1mm时的阀碟上2个测点压力波动时域图，2图中右侧同时标明了阀碟位移方向。由图5可以看出当阀碟顶端振幅为0.6mm时，阀碟上压力测点波动仍呈现随机状态，并未受到阀碟运动的影响。而由图6可以看出，当阀碟顶端振幅为1mm时，阀碟监测点压力明显出现了随阀碟位移变化的周期性波动现象。当阀碟运动到东侧时，位于东侧的监测点A1的波动明显增大;当阀碟运动到西侧时，位于西侧的监测点A2的波动明显增大。

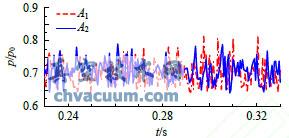
图4 两监测点压力波动时域图(阀碟固定)

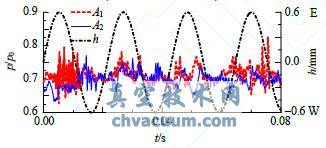
图5 两监测点压力波动时域图(h=0.6mm，f=46.4Hz)

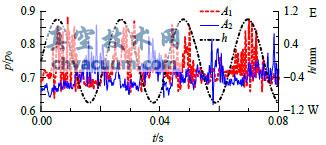
图6 两监测点压力波动时域图(h=1mm，f=46.4Hz)

　　图7为在计算中调节阀沿进口方向中心截面上三种典型的流型。可以看出从两侧喉部流出的高速射流在阀碟下方区域某点撞击后向出口流动。跨音速撞击射流自身的不稳定性使得喉部以后的射流处于不断的摆动状态，撞击点也在阀碟下方不断移动。当由撞击形成的高压区移动到监测点附近时就会导致监测点处压力脉动增加。当阀碟处于静止状态时，由两侧喉部流出的高速射流的强度相当，高速射流在阀碟下方撞击后不会出现射流角度发生较大偏斜的流型，撞击位置相对远离阀碟下方，所以阀碟监测点处不会出现明显的压力波动。而当阀碟在振动中偏向一侧时(如图2中阀碟偏向东侧为例)，由西侧较宽的喉部处有更多的流体流过，此时由西侧喉部流出的流体具有更多的能量推动由东侧喉部流出的高速射流偏向东侧，撞击点也会更接近监测点A1处，导致A1处压力波动增大。同样当阀碟偏向西侧时，高速射流撞击点位置也会转移到A2附近，所以A2的压力波动也会相应增加。

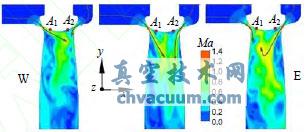
图7 调节阀沿进口中心面Ma图

　　由图4—6可以看出，当阀碟顶端的振幅小于等于0.6mm时，数值模拟此调节阀内流动可以不考虑阀杆系统振动对流场的影响。但当阀碟顶端振幅达到1mm时，阀内的流动明显受到阀杆系统振动的影响，此时须对其加以考虑。阀碟顶端振幅主要由阀碟和阀碟套间隙决定，当这一间隙足够大时，阀杆系统的振动就会引起调节阀内流场周期性波动，形成流固耦合振动，这种振动往往严重威胁调节阀的安全。

　　图8和图9为阀碟顶端振幅为h=1mm，振动频率分别为f=92.8Hz和f=185.6Hz时的阀碟两测点压力波动时域图。当阀杆系统按照92.8Hz振动时，两测点压力脉动仍随阀碟位移有明显的周期变化，但压力波动已出现了滞后现象。当按照185.6Hz振动时，阀碟测点处虽出现了较大幅度的压力脉动，但和位移已没有明显的周期对应关系。这是由于两侧高速射流的摆动存在惯性，随着振动频率的增加两侧射流难以及时跟随阀碟一起运动，所以在监测点处也不会呈现明显的随阀碟移动的压力波动。

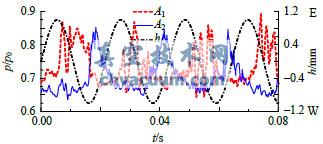
图8 两监测点压力波动时域图(h=1mm，f=92.8Hz)

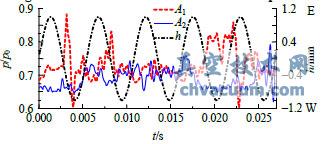
图9 两监测点压力波动时域图(h=1mm，f=185.6Hz)

4、结论

　　本文利用FLUNT中动网格模型和UDF函数，考虑了阀碟在不同振动幅值和振动频率下对阀内流场的影响，得到如下结论：

　　1)在动网格变形中，采取固定阀碟边界层处附近的网格使网格在尺度相对较大的位置移动变形。避免了以往动网格变形中由于边界层网格畸变过大而导致的计算发散。这种高质量的网格变化方法对调节阀内利用动网格模拟阀碟移动对阀内流场的影响有重要意义。

　　2)动网格计算表明当阀碟顶端振动幅值小于等于0.6mm时，阀碟上压力波动为随机波动;当阀碟顶端振动幅值达到1mm时，阀碟上压力波动呈现随阀碟位移周期性变化的特点，此时数值计算中应考虑到阀杆系统振动对流场的影响。

　　3)随着阀杆系统振动频率的增加，由于主流流型变化存在惯性，阀碟上的压力波动随阀碟位移出现滞后现象直至周期性波动消失。数值模拟了阀杆系统按照不同振幅和振动频率对阀内流场的影响，对后续数值模拟中是否考虑振动对阀内流场的影响提供了参考。