恒流量控制阀结构优化及流场数值仿真
针对现有的机械自力式恒流量控制阀阀芯受力-位移曲线在小位移范围非线性变化的问题,影响流量的稳定性。为解决上述问题,对恒流量控制阀阀芯、挡环进行结构改进,并利用二维数值仿真技术对改进之后的流场进行计算,最终得到了阀芯受力-位移曲线呈线性变化的控制阀模型。为了验证二维数值仿真结果的可信性,对包括出口支撑板在内的控制阀全流场进行三维数值仿真计算。结果可知,阀芯和挡环的结构以及支撑板的位置对恒流量控制阀的阀芯受力有一定影响。同时,通过三维流场数值仿真证明,采用二维流场数值仿真即可较好地得到控制阀的流场特性。
1、引言
在航空航天、机床液压、空调、供水、灌装等系统中大量使用恒流量控制阀,来使得在外负载变化的时候,仍然能够维持控制阀流量的恒定,从而稳定执行机构的运行速度。恒流量控制阀在国外已经有30多年的应用历史,但是在国内尚未大量普及,相关的研究也很少。
机械自力式恒流量控制阀是典型的恒流量控制阀,专门用于需要恒流量控制的流体管网系统。目前已公布的机械自力式恒流量控制阀构造趋于一致,它们的共同缺点是流场复杂,通流面积小,流阻大等。
林雄伟等人创新设计了一种机械结构简单,通流能力强的机械自力式恒流量控制阀,但存在阀芯受力-位移曲线(以下称为F-x曲线)在小位移范围非线性变化的问题,难以满足阀芯在全位移范围(即0~15mm范围)的F-x曲线最大线性拟合误差小于5%的设计要求。本文将在林雄伟研究的基础上,通过对阀芯和挡环进行结构改进,使阀芯F-x曲线最大线性误差满足设计要求。
2、恒流量控制阀原理
恒流量控制阀的基本结构还是节流口,通过节流口的流量通用公式为:
其中:
K———节流系数,由节流口形状和流体性质决定; A———节流口的通流面积; Δp———节流口前后压力差; m———节流口形状和结构决定的指数。
在外界压力变化时要想保持系统流量恒定,一种方法是利用压差补偿装置使节流阀前后的压差保持不变;另一种方法是在节流阀前后压差变化时,自动调整节流口通流面积A,目标是使AΔPm的值保持不变。林雄伟便是根据第二种方法设计的恒流量控制阀模型,如图1所示,其主要零部件有阀芯、支撑杆、挡环、线性弹簧和出口支撑板。
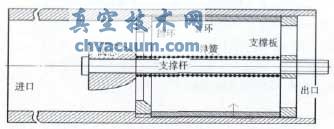
图1 恒流量控制阀模型
阀芯套在支撑杆上,在流体对其施加的向右的流体作用力和弹簧施加的向左的弹簧力共同作用下在支撑杆上左右滑动,当此二力相等时阀芯停止运动,控制阀达到平衡状态,此时通过控制阀的流量即为目标控制流量。由于该模型采用的是线性弹簧,因此在平衡状态下,
F=k(x+xini) (2)
其中,F为阀芯所受流体作用力,k为弹簧刚度,x为阀芯向右的位移(图1所示位置时阀芯位移为0),xini为阀芯位移为0时的弹簧预压缩量,x和xini的和即为弹簧压缩量。
根据式(2)可知,要求所设计的阀门能够自动且合适地调整阀芯位置,从而实现恒流量控制功能的必要条件是:在某一恒定进口流量下,阀芯所受流体作用力随阀芯位移呈线性变化。本文也将以此作为判定控制阀能否在外负载变化时自动维持其流量恒定不变的准则。
阀芯所受流体的作用力与阀芯前后表面流体的压力有关,根据式(1)可知,在固定流量的情况下,阀芯前后的压力又和阀芯与挡环所构成的节流口通流面积相关,所以,合理设计不同阀芯位置时的节流口通流面积是重点。由于挡环内径一定,因此,研究重点最终转化到阀芯的几何曲线的设计上。
3、恒流量控制阀的阀芯曲线设计
根据分析,由于本文中的节流口形式与同心圆环缝隙较接近,因此采用同心圆环缝隙流量公式对阀芯几何曲线进行设计:
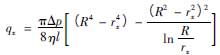 (3)
(3)其中,η为流体的动力粘度,l为同心圆环的重合长度,rx为同心环内圆环半径,即阀芯曲线纵坐标,R为同心环外圆环半径,即挡环内圆半径。
要想搭配线性弹簧实现恒流量的目的,则要求当阀芯在位移x处平衡时:
ΔpxS=k(xini+x) (4)
其中,Δpx为阀芯位移为x时节流口前后的压差,S为阀芯最大横截面。
结合式(3)和式(4)得到
 (5)
(5)其中:
r0———阀芯最右端截面半径,取为5mm。
利用matlab反函数求解功能对式(5)进行求解,得到控制阀芯的几何曲线坐标rx,如图2所示。下文将以此作为原始模型的阀芯结构,其它零件尺寸参照,对原始模型的流场进行数值仿真分析。
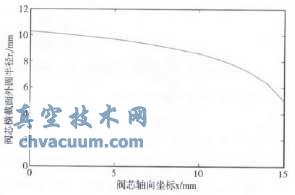
图2 阀芯几何曲线坐标图
4、二维数值仿真及优化
4.1、原始模型的数值仿真和分析
原始模型中忽略支撑板对流场的影响,采用效率较高的二维轴对称模拟方式,对恒流量控制阀的流场进行数值仿真,可以节省实验投入。计算区域为阀前3×D到阀后6×D。阀芯前后1×D的区域为整个流场中物理量变化最剧烈的部分,因此阀体网格分三段处理,对阀芯部分加密,整体都采用结构化网格,计算采用SIMPLE算法,湍流模型采用RNG模型。
边界条件上,流动介质选择常温常压下的水,入口采用1m/s恒定速度,从而保证了进口流量的恒定;出口边界条件为压力出口;收敛条件为:Continuity、X-velocity、Y-veloci-ty、Z-velocity、K、Epsilon残差均小于10-5。
对阀芯位移分别为0mm,1mm,2mm,……15mm时计算阀芯受力,最终得到阀芯F-x曲线如图3所示。
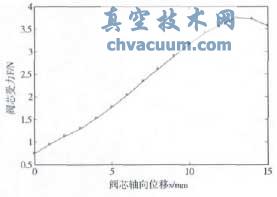
图3 原始模型阀芯F-x曲线
根据前面的分析,要达到恒流控制的要求,阀芯的受力应随阀芯的位移呈线性变化。但由图3可以看出,在阀芯F-x曲线中,阀芯位移在0~5mm范围内力的增长率稍小,当阀芯位移在11mm~15mm范围内出现增长率减小甚至为负的情况,显然无法达到线性变化的要求。针对这个问题,下面将对阀芯和挡环这两个涉及节流口结构的零件进行改进。
4.2、阀芯结构的改进
由于原始模型的阀芯最左端的几何曲线突然消失,流场发生突变,原有的趋势没能得以延续,从而影响了阀芯大位移范围时的受力情况,导致阀芯F-x曲线末段呈非线性。因此在阀芯左端增加一定长度,将有利于维持其附近流场的延续性,本文增加了6mm的斜线段,其斜率与原始阀芯曲线最左端的斜率一致。将这一改进的模型称为模型1;
对模型1进行数值仿真,得到其流场情况,图4为原始模型和模型1的阀芯在位移15mm时的流场速度矢量对比图。
由图4可知,模型1在阀芯左端增加了6mm的斜线段,使得阀芯在大位移时节流口附近的流场更加光顺,延续了阀芯位移为5~11mm时节流口附近的流场规律。
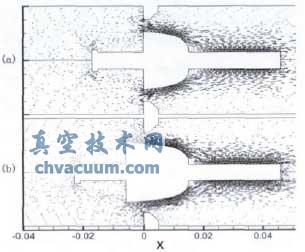
图4 阀芯位移15mm时的速度矢量对比图
图4中,(a)为原始模型速度矢量图,(b)为模型1速度矢量图。
计算得到阀芯的F-x曲线如图5所示。在阀芯左端增加6mm的斜段,阀芯大位移范围的F-x曲线线性度有很大改善,与中段位移部分的增长率保持了较好地一致性。
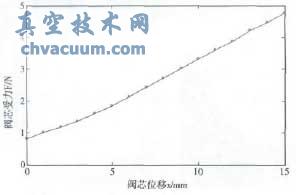
图5 模型1的阀芯F-x曲线
但是,阀芯F-x曲线在阀芯位移0~5mm范围的增长率小于5~15mm范围的增长率,整体仍然没有实现线性增长的目标。下文将对挡环结构进行改进,减小阀芯在大位移范围内的受力,以实现阀芯F-x曲线在0~15mm范围整体线性度良好的目标。
4.3、挡环结构的改进
挡环与阀芯组合在一起构成圆环形节流口,流体通过节流口之后压力降低,节流口之后扩展部分的结构决定了流体通过节流口之后的流场情况。
扩展部分的长度没有一定的标准,主要依据经验而定,如选择过短,流体通过节流口之后扩张过快,容易引起扰动,产生紊流,从而造成内部摩擦损失,使流体压力减小;如选择过长,则流体与壁面摩擦损失增加,也会造成流体压力减小。模型1中的挡环厚度为5mm,当阀芯位移小于5mm时,扩展部分的长度由阀芯位移决定;当阀芯位移大于5mm时,扩展部分的长度等于5mm,固定不变。因此扩展部分的长度变化趋势在阀芯位移为5mm时发生了改变,这一点在图5的阀芯受力曲线上得到了验证。所以,适当增加挡环厚度,延续节流口后的扩展部分长度的变化趋势,将有利于延续阀芯受力曲线的变化趋势。
另外,由于挡环结构的原因,在节流口后靠近挡环内壁的区域出现真空区,真空区对流体产生抽吸作用,使流体流速增大,压力减小。图6为阀体内部流场的压力云图,图6(b)、(c)所示为挡环下方真空区的压力云图和速度矢量图。在控制阀进口压力不变的情况下,真空度的大小取决于挡环内壁的斜度。所以,适当增加挡环内壁的斜度,减小真空度,将有利于削弱真空区对流体的抽吸作用,降低流体流速,从而增大节流口之后的流体压力,使得阀芯大位移范围时的受力减小,最终提高阀芯受力曲线的整体线性度。

图6 挡环后的真空区
因此,可在模型1的基础上对挡环的厚度和内壁的斜度进行改进,具体如下:
模型2:在模型1的基础上,将挡环的厚度由原来的5mm增加到9mm;
模型3:将挡环厚度由9mm增加到13mm;
模型4:在模型3的基础上,将挡环内圆柱面改为圆锥面,倾斜角为5°,其内圆半径左大右小。
对这三种模进行数值仿真计算,得到阀芯在各个位移时的流场情况。
图7为四个模型在阀芯位移为15mm时的流场压力云图对比。
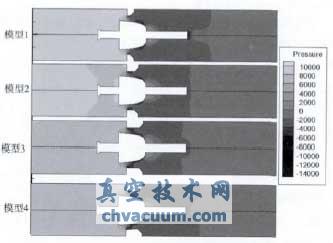
图7 阀芯位移15mm时的流场压力云图
由图7可知,模型2仅仅将挡环厚度增加了4mm,控制阀左右两端压力变化不大;模型3进一步增加了挡环厚度,模型4在将挡环内圆柱面改为圆锥面,可以看出控制阀进口压力减小,因而阀芯受力会减小。
将四个优化模型所计算得出的阀芯F-x曲线进行对比,如图8所示。
由图8可见,将阀芯和挡环进行优化后,所得到的的模型2、3、4都基本实现了阀芯F-x曲线全位移范围呈线性变化的目标。
对这三种模型所得到的的F-x曲线进行线性拟合,可得每一条曲线的最大线性拟合误差,结果见表1。
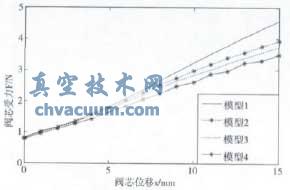
图8 四个模型的F-x曲线对比
表1 F-x曲线的最大线性拟合误差

由表1可知,模型4所得到的阀芯F-x曲线的最大线性误差最小,并可满足小于5%的设计要求。
5、三维数值仿真及优化
二维数值仿真虽然简单快速,但能否反应真实的流场情况还有待验证。同时控制阀模型中的支撑板由内、外圆环体和三条筋组成,如图9所示,它对流场的干扰是否会对二维结果造成较大影响,还需经三维数值仿真进行检验。

图9 恒流量控制阀三维模型
5.1、网格划分与数值仿真
本文采用ANSYSICEMCFD提供的先进的O型结构化网格对恒流量控制阀的三维模型进行离散化处理。
计算区域仍采用阀前3×D到阀后6×D的区域;对阀芯前后1×D的区域轴向和径向加密,周向不加密。同时为了更准确的模拟支撑板对流场的阻滞效应,对支撑板前后5×c的区域再进行周向加密,其中c为支撑板连接筋板的厚度。最终得到的网格如图10所示。计算仍采用SIMPLE算法,湍流模型采用RNGk-ε模型。
5.2、结果与分析
支撑板到挡环安装止口的距离为L,如图11所示。分别计算当支撑板位置在L=36mm、32mm、28mm、25mm时的控制阀流场情况,如图11所示为它们的压力云图对比。

图10 恒流量控制阀三维结构化网格划分
由图11可知,支撑板前缘有一个高压区,说明支撑板对流场具有一定的阻滞效应。当支撑板到阀芯的距离变小时,其阻滞效应所产生的高压区慢慢靠近阀芯右端,并与阀芯右端的流场相互融合,使得阀芯右端的高压范围慢慢增大。
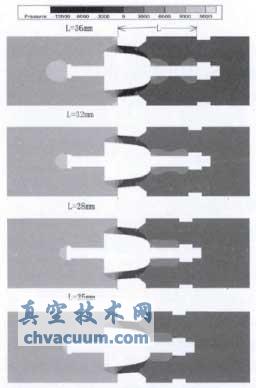
图11 支撑板不同位置时控制阀压力云图
计算得到支撑板处于四个位置时阀芯位移为0mm~15mm的阀芯受力情况,并与简化二维轴对称计算结果相比较,如图12所示。
由图12可知,三维数值仿真与二维数值仿真的结果虽然有一定差别,但总体趋势吻合较好,验证了恒流量控制阀的简化二维轴对称数值仿真结果的可信性。同时通过三维数值仿真所得到的阀芯F-x特性曲线总体也保持线性增长趋势,说明该流量阀在搭配线性螺旋弹簧时,能够很好地实现恒流量控制功能。
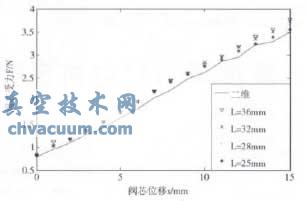
图12 恒流量控制阀三维与二维模拟结果对比
另外,由图12中还可以看出,L=25mm对应的控制阀模型在阀芯位移较大时其受力相对其它的模型有些许变小,这是由于支撑板过于接近阀芯,其对流场的阻滞作用对阀芯右侧表面的影响太大,使得阀芯右侧表面的压力偏大,因而阀芯受力会变小。
计算得到支撑板处于四个位置时所得到的阀芯F-x曲线最大线性拟合误差如表2所示。
表2 不同支撑板位置时阀芯F-x曲线的最大线性拟合误差

由表2可知,在逐渐减小支撑板与阀芯之间距离的时候,可以利用支撑板对流场的阻滞作用对阀芯F-x曲线进行适当微调,以提高其整体线性度,从而提高恒流量控制阀的控制精度。但是如果该距离太小,阻滞作用对阀芯受力的影响太大,阀芯F-x曲线的整体线性度反而会变差,例如当L=25mm。因此,支撑板的最优位置在L=28mm处,此时,阀芯F-x特性曲线的线性度最好。
6、结论
1)阀芯几何尺寸以及挡环的结构均对恒流量控制阀的控制性能有重要影响,这两部分的结构设计至关重要;
2)支撑板对流场有一定的阻滞作用,其位置对恒流量控制精度有一定影响;
3)较简单的二维轴对称数值仿真能较好地反应恒流量控制阀的流场特性,其结果可以作为恒流量控制阀设计的依据。






