真空断路器灭弧室内真空度与介电常数联系机理研究
真空断路器是中压配电开关中的核心类型,真空灭弧室的真空度是影响其运行质量和寿命的重要因素。伴随着国家智能电网和基于可靠性检修体制的不断发展,在线监测灭弧室真空度成为智能断路器的新要求。基于耦合电容法的真空度在线监测方法是目前较为普遍使用的一种监测方法,利用耦合电容传感器探测灭弧室屏蔽罩电位Uc的变化实现,而感应电位Uc与灭弧室气压下灭弧介质的介电常数εr密切相关。本文对灭弧室气压值P(真空度)和εr的关系进行研究,并推导了干空气条件下P 和εr的关系公式,为进一步分析真灭弧室真空度P 和屏蔽罩电位Uc 联系机理提供了研究基础,希望在理论上为进一步提高耦合电容传感器实用技术作支持。
研究背景
真空断路器近三十年来在我国中压开关产业不断发展,其应用范围日渐增大。并具有体小、重量轻、适用于频繁操作、灭弧不用检修的优点,在中压配电领域开关中占有主导地位。而一旦真空断路器发生故障极易引起十分严重的后果,不仅会引起自身设备损坏,更有可能引发大规模电网故障。真空断路器的故障往往是由于真空度降低所致,根据国家规定,真空灭弧室内的气体压强应低于1.33×10-2 Pa。由于真空灭弧室存在缓慢漏气现象,真空度会随着使用时间的延长呈现持续降低的趋势,当到达某一临界阈值时,就会引发安全危险隐患。智能电网对真空度监测的要求逐渐提高,真空技术网(http://www.chvacuum.com/)建议使用中的真空断路器采用实时监测,特别是对于35 kV、72.5 kV 及以上电压等级的真空断路器采用在线监测手段及时掌握灭弧室真空度状况更具实用价值和意义。
根据动态电荷分布和电容分压原理构建的耦合电容法具有探头结构简单,安装简便,抗干扰能力好等优点。其应用于实际检测的过程,往往需要先在实验室条件下标定某特定型号真空断路器的耦合电容传感器输出电位的变化趋势与其灭弧室真空度值相对应的关系曲线,再将该标定曲线应用于实际检测。此过程只能定性的利用真空度变化对屏蔽罩电位产生的影响,并且真空度劣化极限对应屏蔽罩电位的阈值需依靠经验数据来确定。为理清真空度与屏蔽罩电位的理论关系,使耦合电容法的实际应用过程不盲目。本文从电介质理论着力,通过介电常数的引入,希望能够将屏蔽罩电位随真空度的变化过程加以解释。
此外,以屏蔽罩电位为监测基础的灭弧室真空度的在线监测方法有许多,如:耦合电容法、旋转式电场探头检测法、光电变换法、比例差分探头检测法等。屏蔽罩电位成分分析的意义显得更加重要。真空断路器实际运行时,屏蔽罩上的电位成分较为复杂,既有直流分量又有交流分量。以下是前人通过实验总结出的真空度降低所导致的屏蔽罩电位的变化规律。
理论上,当真空灭弧室内真空度正常时,仅需几百伏的电压就可维持带电触头与中间屏蔽罩之间由场致发射引起的电子电流,屏蔽罩积累的负电荷使其负电位几乎达到电极电压峰值;当灭弧室内真空度劣化时,其气体密度变大,场致发射的电子被气体分子吸附后成为负离子,而负离子质量大,漂移速度慢,使得上述电子电流减小,屏蔽罩上由场致发射导致的电位降低。此外当真空灭弧室的运行电压和内部真空度处在正常范围时,灭弧室的屏蔽罩上不带有静电荷;当真空度下降导致绝缘强度降低时,触头与屏蔽罩之间会发生局部放电,使灭弧室的屏蔽罩上带有一定量的静电荷而形成直流电位。文献得到的结论认为:真空度下降到一定值时屏蔽罩上形成的交流电位幅值会发生变化,同时屏蔽罩上还会有直流电位生成。两种电位的变化都是由于在真空度下降时金属导杆和触头电极与屏蔽罩之间出现的汤森放电所导致,并且电位变化时对应的真空度相同。
本文就宏观电介质理论中影响电气绝缘材料性能的最主要参数相对介电常数进行讨论,并将讨论结果应用于电磁场数值计算。其中,感应电位的求解分析,对真空度在线监测理论的深入探讨有着十分重要的意义,深入探索灭弧室内真空度与屏蔽罩上感应电位的内在联系机理是本文的研究重点,该问题的解决不仅能够为耦合电容法提供理论依据,更能为诸多通过监测屏蔽罩上的感应电位实现真空断路器灭弧室真空度在线监测的方法提供理据上的理论支持。
1、灭弧室真空度与屏蔽罩电位的关系模型
现代计算机技术的发展使得建模仿真软件与数值模拟方法能够方便地应用于处理超大计算量的数值计算及复杂物理模型的仿真分析。本文研究基于电磁场仿真软件Ansoft,对真空灭弧室内的真空度和屏蔽罩电位对应的关系进行分析,力求找出二者之间的内在联系机理,为实现真空度的在线监测和状态评估提供理论基础和技术支持。为分析方便,将处于工作状态下的灭弧室物理模型图构建如下。

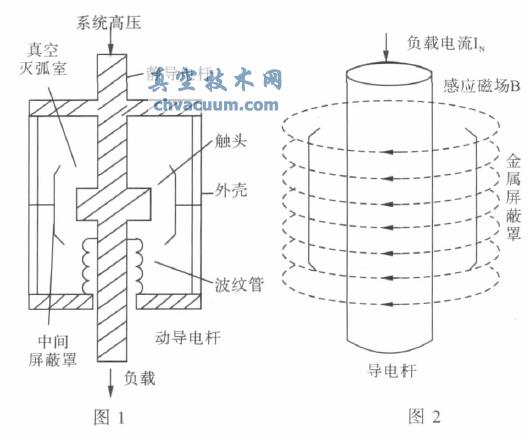
图1 真空灭弧室运行状态下物理结构模型 图2 真空灭弧室运行状态下抽象模型
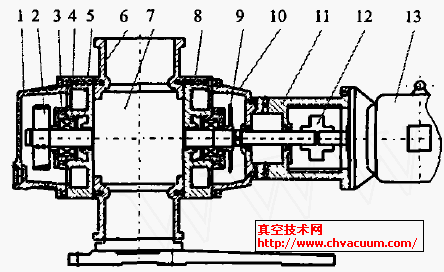
如图1 所示,真空断路器两触头在额定交流负荷电压下工作,通过导电杆和触头的交流激励电流必然会以两触头为轴心产生环型磁场,该磁场将在真空为介质的金属屏蔽罩上产生出一系列感应电位。分析该物理过程的抽象模型,等价于求解通有额定交流电流IN 的金属圆柱体在真空环境下对外环金属屏蔽罩上的感应电压。其抽象模型如图2所示。
在图2中导电杆中通有额定负荷电流IN,感应磁场方向符合安培右手定律。求解该模型,需求解触头在负载电流IN 条件下,周围真空区域的磁场分布情况,及处于该磁场下金属屏蔽罩上的感应电位Uc。
2、灭弧室真空度与介电常数联系机理分析
在上述模型求解的过程中,真空灭弧室内中间介质的介电常数εr 无疑是一项重要的条件参数。考虑到真空灭弧室采用真空环境作为中间绝缘介质,即低压空气。笔者经过细致检索发现,低压空气介电常数εr 与压强P 物理联系的文献资料较少,难以直接得到某真空度P 下对应的精确εr。因此本文工作希望建立物理数学模型得出低压空气和相应介电常数的联系关系,从而得到P-εr- Uc 的对应关系(其中为屏蔽罩上的感应电位)从而为真空断路器灭弧室真空度的在线监测提供理论和技术上的支撑。
2.1、克劳休斯-莫索缔方程
引用电介质物理中克劳休斯- 莫索缔(Clausius-Mossotti)方程,简称克- 莫方程。该方程在洛伦兹有效电场条件下,联系了电介质极化的宏观参数和微观参数。其数学表达式如公式(1)所示:

式中:εr、ε0分别为气体介质的相对介电常数和真空状态下空气介电常数;α 为空气分子极化率;n0为电介质单位体积内的极化粒子数。摩尔体积与单位体积内极化粒子数的关系转化可得下式:

其中,M和ρ分别为电介质的摩尔质量和密度,N0为阿佛加德罗常数。在公式2中[P]代表了摩尔极化过程,式子右端表明,对于某固定电介质,当极化率α 有确定的值,并且与密度ρ 无关时,[P]为确定常数。左端式子表明,摩尔质量固定,当[P]为常数时,εr-1/εr+2与密度ρ成比例关系。通常介电常数εr随着电介质密度ρ 的增大而增大,其物理意义也较容易理解,因为随着电介质密度ρ增加,单位体积内极化粒子数增多,故介电常数εr也随着电介质密度ρ增大而增大。既然εr-1/εr+2与密度ρ成正比,不妨设比例系数为L。则有:

至此,得出了空气密度和介电常数的关系,进而将灭弧介质(空气)的密度转换为气体压强便可以得到真空度和介电常数εr的关系。
2.2、干空气密度与压强的关系的建立
空气的密度的国际定义式为:

式中:m0是空气的质量,单位kg;V是空气的体积,单位m3;ρ 单位为kg/m3。空气密度与空气压力、温度及湿度有关,本文将空气假定为干燥空气(此种假设符合真空灭弧室的实际工作条件)。公式(4)只是关于气体密度的一般定义式,在通风工程中,干、湿空气密度是由气态方程求得。气态方程表达式为:

式中:ρ、ρ0 分别为特定状态(非标准状态)及标准状态下干空气的密度,单位kg/m3;P、P0 分别为特定状态(非标准状态)及标准状态下空气的压强,单位kPa;T、T0 分别为特定状态(非标准状态)及标准状态下空气的热力学温度,单位。标准状态下,T0=273 K、P0=101.3 kPa 时,组成成分正常的干空气的密度ρ0=1.293 kg/m3。将这些数值代入公式(5),即可得到干空气密度ρ 的计算式为:

使用上式计算干空气密度时,应注意压强、温度的取值,式中P 为空气的绝对压强,单位为kPa;T 为空气的热力学温度,单位为K;T=273+t,t为空气的摄氏温度,单位为℃。将公式(6)代入公式(3)可以得到:

对公式(7)进行分析可知,当温度恒定时,只有P 和εr 两个变量,可设一常量Q= 3.48LT并将其代入公式(7),可得:
![]()
由此可以得到介电常数εr 的表达式如下:

已知标准大气压强,P0=1.013×102 kPa, 空气相对介电常数为εr=1.0005548,将其代入公式(9)可以得到Q=1.825×10-6。故公式(9)又可以写成:

于是,可以得到干空气条件下真空度P 与空气介电常数εr 的确定对应关系。
2.3、真空度与介电常数的关系验证
文献中列举了一组通过把干空气介电常数εr 转换为波长测量得到的值。由公式(11)计算得到的P- εr 值也在表1 中给出,以方便与文献的结果进行对比。如表1 所示为干燥空气条件下,压强P 和介电常数εr 的对应关系数据。
表1 干燥空气压强P与相对介电常数εr 对应关系

经过验证,干燥空气介电常数εr 的计算值与实验测量结果非常接近,相对误差很小。因此根据公式10 得出的压强与相对介电常数的关系,可以作为进行进一步仿真模型建立的参数条件使用,将仿真分析所需真空压强值代入公式,即可得到对应的相对介电常数值。计算实际灭弧室内压强范围对应的介电常数值于表2。
表2 灭弧室内压强范围对应干空气相对介电常数

这样便为进一步得到灭弧室内真空度压强与屏蔽罩电位的对应函数关系表达奠定了条件基础,作为真空断路器灭弧室真空度在线监测和状态评估的特征检测变量据理才能更为充分,本文工作可以为真空断路器真空度在线监测技术应用提供理论和技术支持。
3、结论
本文针对电力系统中广泛应用的真空断路器的核心部件之一真空灭弧室的在线监测的机理问题展开研究,以耦合电容法作为在线监测真空度手段。通过工作条件下的真空灭弧室的实际工作条件分析,为屏蔽罩电位检测为途径的真空度在线监测方式提供依据,建立了简化的真空灭弧室真空度在线监测物理模型,引入电介质物理学和高电压工程中的克劳休斯- 莫索缔方程,建立了真空灭弧室内真空度P 与相对介电常数εr的物理联系,并给出了相应的表达式。以电解质的相对介电常数εr 为中间变量,可见建立真空灭弧室内真空度P 与屏蔽罩上感应电位的联系机理。通过Uc 的连续在线检测便可以实现真空断路器灭弧室真空度的在线监测和状态评估。虽然在分析过程对模型做了必要的简化,本文研究工作为真空断路器的智能化和状态检修提供了必要的理论和技术支持,具有较好的借鉴价值。