质谱计离子源静电透镜的模拟计算

　　本文针对某质谱计离子源的设计，建立了离子源静电场数学模型，采用有限差分法对其场域进行离散，半迭代切比雪夫松弛法求解各节点的电位，拉格朗日插值法计算空间任意点的电位和电场，四阶龙格- 库塔法计算离子运动轨迹。使用Visual C++ 6.0 为平台编程计算程序，结合离子源的具体结构求解了离子源静电透镜整个场域的电位和电场；绘制了等位线和离子运动轨迹。在此基础上，讨论了各极电压对离子运动轨迹（即对聚焦性能）的影响。

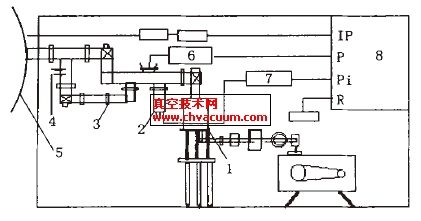
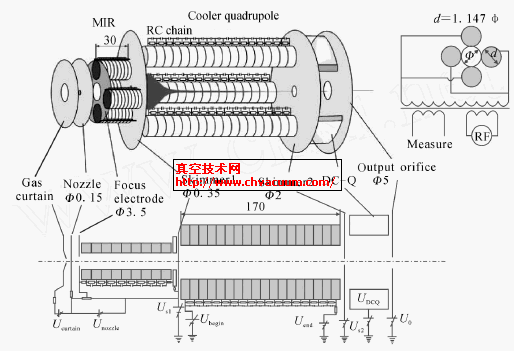
　　质谱计尼尔型离子源^[1]主要由电离室、灯丝和离子静电透镜组成。灯丝发射出的电子在加速电压和外加磁场的共同作用下，加速后螺旋运动经过电离室。在电离室中，运动电子碰撞气体分子使其电离，电离后的气体正离子被离子光学系统引出并聚焦，最后进入质谱计分析器中，多次碰撞后的电子被相对电离室电位为正的的收集极所收集。

　　质谱计离子源通过静电透镜实现离子束的聚焦，在电极几何结构一定的情况下，不同电极电位下离子透镜的聚焦性能不一样。由于电极电位可调范围宽，用试验的方法寻找最佳聚焦电位比较困难，需要对离子源透镜的静电场进行模拟计算为试验调节及优化几何尺寸设计提供指导。然而，考虑到离子源离子透镜边界形状的复杂性和拉普拉斯方程组的自洽性，很难解析求解拉普拉斯方程组和离子运动方程。因此，需要采用数值计算方法来计算离子源的电场分布和离子运动轨迹。

1、离子源静电透镜静电场数学模型的建立及求解

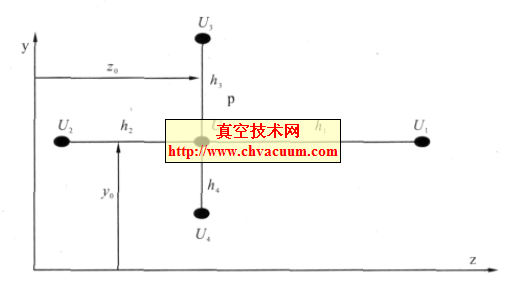
　　离子源离子静电透镜电极呈狭缝膜片状，具有面对称特性（属于柱面透镜），是带状离子束的聚焦系统，相当于光线光学中的柱形透镜。由于柱形场是横向单向对称、横向单向退化的场，因此具有以下的特点^[2]：

　　（1） 它的场分布和电位（标位）分布均与一个横向坐标无关（例如对称面为x- y 面），因此等位面是一系列柱面族，沿柱面延伸的方向（即x方向）场强为零。

　　（2）它的电位分布有一个横向对称面。因此在这个对称面中垂直于该面的场强为零，也即等位面与此对称面正交，并且这个对称面平行于柱面延伸的方向。

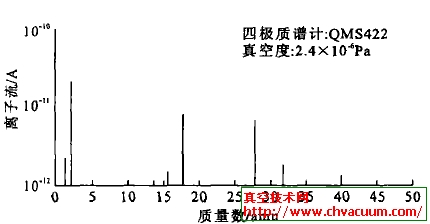
　　质谱计离子源内离子流强度较弱^[3]，离子束对空间电场的影响较弱可忽略不计，因此质谱计离子源离子透镜电场的计算属于拉普拉斯方程组求解问题。

　　静电场的数值计算方法主要有：有限差分法、有限元法和边界元法^[4]。其中有限差分法是分析电场问题的一种重要方法。有限差分法的基本思想就是将待求解的场域用网格划分出来，再把拉普拉斯方程用各网格节点的电位作为未知数的差分方程进行代换。有限差分法直观、理论成熟、精度可选、易于编程、易于并行，所以本文采用有限差分法来求解离子源静电场。

1.1、空间场域离散和迭代求解

　　离子源静电场的拉普拉斯方程用（1）式表示：

　　求解方程（1）的方法是将求解的区域用直线划分为许多（有限个）正方形或矩形网格；用与这些网格相邻节点的差分方程来代替偏微分方程，建立与所有节点电位对应的线性方程组；求解线性方程组，得出该区域的电位分布。

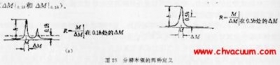
　　采用将一个网格节点的电位与其最近邻的四个网格节点的电位联系起来的五点差分格式建立差分方程，如图1 所示。

图1 差分法求解电位示意图

3、小结

　　本文对离子源静电场计算和离子轨迹模拟方法进行了介绍；以Visual C++ 6.0 为平台，采用有限差分法和半迭代切比雪夫松弛法计算了拉普拉斯方程，得出了静电场电位分布；用拉格朗日插值法描绘了空间电位及等位线；采用四阶龙格- 库塔法模拟了离子运动轨迹。质谱计离子源离子透镜模拟计算为该结构尺寸的离子源静电透镜各电极电压的选择提供了有力支持，对提高离子聚焦性能发挥了重要作用。

参考文献

　　[1] Nier A O, Schlutter D J . High- performance doublefocusing mass spectrometer [J]. Rev. Sci. Instrum., 1985,56(2):215- 219.
　　[2] 华中一，顾吕鑫. 电子光学[M]. 上海：复旦大学出版社，1999.
　　[3] 季欧，李玉桂. 质谱分析法[M]. 北京：原子能出版社，1988.
　　[4] 陈文雄，西门纪业. 电子光学基础[M]. 北京：北京大学出版社.
　　[5] 邹筝，康晓林，袁建洲, 等. Visual C++ 6.0 实用教程[M]. 北京：清华大学出版社，2005.