真空介电常数与宇宙背景温度的关系

　　根据理想气体状态方程，定义了真空背景周期，计算表明真空背景周期在数值上近似等于真空介电常数。基于点电荷的电场、电阻定律和位移电流假说，探讨了真空介电常数与宇宙背景温度的关系。

1、引言

　　真空介电常数，又称为真空电容率，或称电常数，是一个常见的电磁学物理常数，符号为 ε0。在国际单位制里，真空介电常数的数值为：

ε₀= 8. 854187817 × 10^-12 F/ m

　　真空介电常数是物理量在度量时引进的常数( 主要是库仑定律中对电荷量的度量) ，根据麦克斯韦方程组，可推知真空介电常数与其它物理常数的关系。

ε₀=1μ₀c²₀

　　其中，c₀是光波传播于真空的光速，μ₀是真空磁导率。上式可作为真空介电常数的定义式。

　　真空介电常数虽然是一个度量系统常数，但如它的定义式一样，这个常数与其它常数或物理量是相关的。由于介电常数本身不是一个常量，与介质的性质有关，真空介电常数也应该与真空有关。本文在宇宙背景辐射的“真空”环境下，与真空技术网(www.chvacum.com)的有关专家探讨了宇宙背景温度与真空介电常数的关系。

2、真空背景周期

　　在宇宙背景下，气压是非常低的，完全满足理想气体的要素，选宇宙空间中任一局域( 长方体或圆柱体)为研究对象，理想气体状态方程可写为：

PV = NKT (1)

　　式中P 是系统的压强，V 表示气体的体积，N 为气体分子个数，K 为玻尔兹曼常数，T 为热力学温度。由于 F = PS，V = Sl，其中 F 为作用在气缸两个平行底面的压力，l 为气缸长度( 即两个平行底面的距离) ，则(1) 式化为：

Fl = NKT (2)

　　由于想想气体状态方程是实验结果，因此(2) 式与实验规律直接相关，等式左右两边都具有能量的量纲。(2) 式可解释为整个系统处在一个保守力场之中，单位横截面上的力密度为 F/S，为上述两个底面间势能的增量，KT 为系统微观粒子的平均动能，NKT 为系统的总动能。(2) 式把系统的宏观能量与微观粒子所具有的平均能量联系在一起，值得注意的是：这个解释不同于能量均分定理。

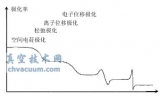
　　对于围绕原子核中心做圆周运动的电子，该电子从所在的能级电离时，所吸收光子的频率(vn) 与电子轨道动能(Ekn) 的关系为：hvn= 2Ekn。考虑真空背景系统，如果 KT 解释为微观粒子的平均动能，则2KT为微观粒子的平均机械能，类比hvn= 2Ekn，有2KT = hv 得:

t =1/v=h/2KT

　　这里t 具有时间的量纲，在真空背景下，我们姑且称之为真空背景周期。已知普朗克常量 h = 6.6262 ×10^-34 kgm².s^-1，玻尔兹常数 k =1.3807kgm²s^-2 k^-1，真空背景温度取为 T =2.725K( T =2.726 ±0.010K)，计算得到真空背景周期 t =8.81 ×10^-12 秒。

3、真空介电常数与真空背景周期的关系

　　值得一提的是，t =8.81 ×10^-12秒在数值上刚好近似等于真空介电常数 ε0，这两个量之间有什么关系呢? 为了说明这个问题，这里假定真空中有二个带有相同电量( 电量为 e) 的点电荷相互作用，相互作用势能为

Ep=e2/ε04πr

　　如果单个电荷以周期 t 做圆周运动，则电流强度为 I = e/t. 根据实验结果，电阻的表达式可写为：

R = ρl/s

　　其中 ρ 为电阻率，l 为介质的长度，s 为介质的横截面积，电流的方向垂直于横截面。对两个点电荷来说，虽然它们“静止”，但它们受“真空背景温度”的影响，也在做轻微的热运动，这个运动可看成是简谐运动( 也可用圆周运动来进行描述) ，运动方向在两个点电荷之间，周期为( 即前面的所说的“真空背景周期”)。运动电荷对应的电流可认为就是位移电流，这种运动使两个电荷间的电场也发生了周期性的变化，变化的周期也为t. 由于位移电流的本质就是变化的电场，则 e/t 在数值上可表示电流的空间分布，电流方向垂直于以 r 为半径的球面，(5) 式中的横截面积为 s =4πr2.

　　由于系统处在真空之中，电阻率很大(相对于导体来说) ，但电子的运动是自由的，两个点电荷间的电阻为：

　R = ρr/4πr²= ρ1/4πr

　　一个电荷相对一另一个电荷的电势 U = IR = ρe/t·1/4πr，相对应的电势能为

Ep= eU = ρ.e²/t4πr

　　比较势能表达式( 4) 式和( 6) 式可知 ε0= t / p，表明真空介电常数 ε0与真空背景周期成正比. 如果假定电阻率 ρ =1，真空背景周期与真空介电常数在数值上完全相等. 根据( 3) 式得：

ε0=h/2KTρ

　　上式说明真空背景温度与真空介电常数成反比，这个结果也显示现实真空环境与宇宙背景有直接关系.虽然用 e/t 来表示位移电流的空间分布并不严格，但是足以说明真空介电常数的测量值与宇宙背景温度有很大程度的关联。

4、讨论

　　本文所讨论的真空是宇宙背景，并不是完全意义上的真空，完全意义上的真空应是自由空间或真空态。当然可实现的真空只能超低压的状态，属于部分真空( partial vacuum) . (7) 式的结论说明宇宙背景温度与真空介电常数有关联，因此准确测定真空背景温度显得非常重要。令人兴奋的是，对真空背景辐射更精确的探测已经展开。 (7) 式还显示真空介电常数与真空电阻率成反比，并且当假定 ρ = 1 时，真空介电常数与真空背景周期在数值上近似相等，因此除了准确测定真空背景温度之外，真空中电阻率的测定也是非常必要的。

　　值得注意的是，文中所讨论的问题与真空背景周期的定义有关，其中 hv =2kT 由来并不严格，式中的频率 v 并非真空背景辐射的频率，此式的更严格的理论说明将在以后的工作中展开。