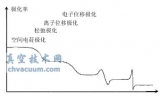
介电常数的基本概念

　　根据静电学的研究成果， 真空中一个孤立的电荷q 会在其周围产生电场E，当另外的一个试验电荷q0 进入到该电场中时会受到电场力的作用。由电荷q 所产生的电场强度为：

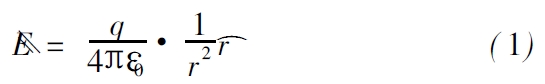
　　其中， ε₀为真空中的介电常数；r 为距离点电荷q 的径向距离。一般来说，电场强度是一个矢量。试验电荷q0 在距电荷q的距离为r 的点上受到的电场力为：

　　根据力的反作用性质，电荷q 也同样受到试验电荷q0所产生的电场的力的作用且作用力的大小相等方向相反。根据式(1) 可知，真空中的介电常数ε₀表征了孤立电荷q 在给定的距离r 上产生的电场强度的大小。如果将式(1) 中的真空条件换为某种电介质， 则同样的孤立电荷q 所产生的电场强度将可表示为：

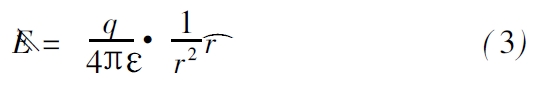
　　其中，ε为该种电介质的介电常数。在实际应用中，人们通常将真空中的介电常数ε₀选作一个参照，而将电介质的介电常数ε与ε₀的比值定义成为一个无量纲的相对介电常数ε_r，如式(4) 所示：

　　由于真空是一个理想的电介质模型( 没有原子、分子) ，所以，在实际电介质中由于束缚电荷效应使原电荷q所产生的电场有所下降的情况在真空中不可能出现。因此, 针对实际电介质的相对介电常数Er 总是满足大于或等于1。

　　由式(3) 可见，介电常数ε表示了电荷q 在电介质中所产生的电场强度的大小的一个制约因素( 除了距离之外，也是唯一的制约因素) 。显然，这种推论在静电场的情况下是完全可以被接受的，但是若要将这一推论直接应用到交变电场的情况似乎还有些不充分。交变电场情况下电介质的微观表现机理与宏观作用的研究取得了一些成果，但是仍然有待更加深入的研究，也是目前电介质物理、量子物理的重要研究方向和内容之一。

　　可以确认的是电介质的介电常数所表征的属性在交变电场的情况下也会对交变电场产生影响。比如，交变电场在电介质中的传播速度会降低, 频率不变，波长会变短( 电磁传播理论)并且介电常数越大，相应的改变也会越大。