路面材料复合介电常数模型研究进展分析

　　路面材料复合介电常数模型是雷达检测路面结构体系含水量、孔隙率、压实度等指标的基础和关键。分析了相关文献的研究成果，剖析了复合介电常数模型的研究现状，讨论了各种模型的优缺点、局限性和适用范围等，论证了进一步研究路面材料复合介电常数模型的必要性。

前言

　　路基路面质量直接影响道路工程的安全和行车的舒适。因此，须对路基路面状况及时检测和评价，以便适时做出科学的决策或采取合理的维修加固措施以确保道路具有良好使用性能。路面探地雷达(GPR)作为一种高效、精确、无损的探测技术越来越广泛地应用于路基路面质量检测方面。路面雷达是基于介质电磁特性的差异进行工作的，当雷达进行路基路面质量检测时，测试中获取的最初和最基本参数是路面材料介质的介电常数，并不能直接测试路面材料的压实度、孔隙率、含水量、沥青含量等质量控制指标，但像路面材料这样由几种不同材料组成的复合介质，其介电常数与复合介质的各组成成分的介电常数和组成比例有关，描述这种关系的式子称为介电常数模型。通过对复合介质介电常数和介电常数模型的研究分析，可间接得到压实度、孔隙率、含水量这些检测指标。因此，研究和建立介电常数与这些指标之间的关系成为了路面雷达技术有待研究的核心内容之一。本文讨论了各种模型的优缺点、局限性和适用范围等，并论证了进一步研究路面材料复合介电常数模型的必要性。

1、研究现状综述和分析

　　路面材料是由固态、气态、液态组成的混合物，是众多复合材料的一种。路面材料复合介电常数模型的复合介电常数反应材料本身的电学性质，由表示介电常数的实部和表示能量损耗与衰减的虚部组成。它与材料各成分的介电常数、含量、温度及频率有关。沥青混凝土、水泥混凝土这些复合材料，其整体所体现出来的复合介电常数也与其骨料、水泥净浆或沥青、空气的介电常数以及体积率有关，而组成部分的体积率与材料压实度、孔隙率、含水量等这些质检指标息息相关，这些指标的改变将直接导致介电常数的实部和虚部变化，例如含水量增加会导致介电常数的实部和虚部增大;孔隙率的减少，即压实度的增加也会使介电常数增大等。国内外，针对复合介电常数与这些质量指标之间的关系开展了不少研究。

　　1.1、经验拟合公式研究现状和存在问题

　　复合介电常数和某一指标间相互关系的经验拟合公式，国内外的学者，都作了相关的研究。首先，对于土壤介电物理特性做出过系统研究的是前苏联学者ChernyakG.Ya.，他在1964年撰写的《湿土介电特性研究方法》(DielectricMethodsforInvestigatingMoistSoil)一书中对含水土壤介电特性作了全面的分析，使人们对土壤介电物理行为第一次有了系统性的认识。1980年加拿大农业土地资源研究中心的Topp利用TimeDomainReflectrometry(TDR)方法测定土水混合物的介电常数，并由此得到了反映土壤含水率w与土水混合物介电常数ε之间关系的两个回归多项式方程，即著名的Topp方程

　　在Topp基础上，美国农业部盐碱实验室Dalton等人测量土壤电导率估计土壤的盐分。Alharath和Ferre先后对粉沙、细沙土进行了实验研究，提出了各自的公式，Roth在他们两人基础上进行适当修正，使得公式的应用拓宽到了沙性土。

　　这些研究成果，特别是针对沙土的成果，为研究混凝土中细骨料的介电特性奠定了理论和试验基础，同时也为分析研究路基土的介电特性提供了参考。但需说明的是上述公式均忽略了介电常数与电磁波频率的关系，并且是在TDR频率范围内测量得到的，而TDR所用的电磁波频率与路面雷达电磁波频率有差异。此外，路基土是压实土，不同于天然土壤，其孔隙率较小。因此，开展路面雷达频率内介电常数模型的研究是非常必要的。

　　1994年，VirginiaTech开展了一项科研项目，对水泥混凝土介电特性进行了研究，分析了水泥混凝土介电特性及其影响因素，分别研究了组成成分、氯化物的含量、混凝土内部损伤、碱硅反应(ASR)、冻融现象对水泥混凝土介电常数的影响，得出了水泥混凝土的介电常数随着水灰比增大而增大等一系列重要结论。1995年，Robertet.al.采用宽带同轴线测量水泥混凝土的复合介电常数，频率范围为50MHz～1GHz，PCC试件骨料最大粒径为15mm和30mm，主要研究了养护时间对复合介电常数的影响。Rhim在1998年也曾在0.1～20.0GHz频率段对混凝土含水量与复合介电常数之间的关系进行了试验研究。

　　为研究热拌沥青混凝土的介电性能，1992年，Al-Qadi研究了其在12.4～18.0GHz频率段内的介电特性，试验采用两种类型的骨料:吸收性较小的石灰石和吸收性较大的砾石，每种类型的骨料都采用两种级配拌和:密级配和开级配，试验建立了热拌沥青混凝土介电常数和含水量之间的相关关系[9]。1999年，Shangetal.采用一种新型装置测量了热拌沥青混凝土介电常数，所用频率为0.1MHz～1.5GHz。浇注试验试件时，采用不同的拌和方式和不同的沥青含量，结果发现沥青含量和拌和方式对所测的介电常数影响不大，而试件的含水量却是重要的影响因素。

　　国内针对水泥混凝土、热拌沥青混凝土和路基土也做了些研究，郑州大学张勇对水泥混凝土和沥青混凝土的介电特性进行了试验研究，研究了龄期内介电常数的变化规律、介电常数与密度、介电常数与强度之间的关系，以及油石比、集料级配、水灰比等参数对介电常数的影响规律。

　　由上述文献综述可知:虽然国内外针对路面材料介电特性进行了研究，但不同的研究者根据各自试验数据提出了不同的经验拟合公式，形式多样，很不统一，若拟合函数选取不同，得出的拟合公式有很大差异，人为主观因素干扰较多，导致公式代表性和适用性差，相互之间可比性也较差。

　　1.2、复合介电常数模型研究现状和存在问题

　　国外对复合介质介电常数模型方面的研究较早，并且做了大量的工作，先后提出了许多复合介质介电常数模型，如经典的瑞利模型(LordRayleigh，1892)、B¨ottcher方程(B¨ottcher，1952)，该模型于1999年被Boersma&vanTurnhout修正，拓展成多相介质体系;Berentsveig公式曾被Leshchanskyi&Ulyanychev于1980年成功地用于100MHz到9GHz电磁波对沙土的介电常数模拟;复折射率法(CRIM)，源于Lichtenecker-Rother(LR)方程CRIM法被Birchaketal.(1974)成功用于两相色散介质复合介电常数的模拟，其使用条件是介质粒径远小于波长(d<<λ)[13]，Whartonetal.(1980)用CRIM法来解释油和气体的复合介电模型;Bruggeman-Hanai(BH)模型与BH方程，是Bruggeman于1935年通过复合介电常数得到，Hanai(1936)修正了Bruggeman方程，并将其用于含有限导电材料的复合介电常数模拟中。以上几种模型中，CRIM模型、线性模型、瑞利模型广泛应用于路面材料方面。

　　国内对介质介电特性和复合介质介电常数模型的研究最早主要集中在微波遥感、地质勘探和石油测井等领域，且研究对象多为水、岩石、土壤等典型天然地物。随着滩地雷达在公路无损检测方面的广泛应用，路面材料介电常数的研究也方兴未艾。中国地质大学的李大心、长沙交通学院的郭云开等人也开展了这方面的研究工作，取得了一定成果。为研究和建立沥青混凝土和水泥混凝土介电常数模型，郑州大学王复明带领的科研团队相继做了两种材料在不同配比下的介电特性试验，对常见的CRIM模型、线性模型、瑞利模型进行了适应性和误差分析，研究发现上述模型需经适当修正才能表征水泥混凝土和沥青混凝土的介电特性。

　　由上面的文献综述看出:国内外对路面材料如水泥混凝土、沥青混凝土、路基土等的介电特性及其介电常数模型的建立做了研究工作，但仍是基于不同试验方案基础上，建立的介电常数模型形式多样，且未考虑温度、频率对其的影响。

　　1.3、介电常数频率依赖性的研究现状

　　探地雷达检测路基路面质量时，因检测目的和目标不同，所选天线的频率也不同，研究发现即使同一种介质在不同频率下其介电常数也不同，即介电常数具有频率依赖性，为研究路面材料介电常数的频率依赖性，查阅相关资料，进行综述分析。针对介电常数频率依赖性的研究较早，其中较为著名的是Debye于1929提出的Debye模型

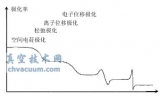
　　式中εs为低频介电常数，又称静态介电常数(f<<1/2πτ)，它表征了松弛极化的影响;ε∞称为介质的光频介电常数或稳态介电常数，也就是材料的高频介电常数，其频率大大高于偶极子的振动频率(f>>2πτ)。τ为弛豫时间，表示介质分子从开始极化到达到极化的最终状态所用的时间，与温度有关。Debye模型可简单表示如图1。Debye方程描述了介电常数随频率变化而改变的宏观趋势，不仅实现了复合介电常数在数学表达式上实部与虚部的频域分解，同时也表明了在外加交变电场作用下介质的静态介电常数εs与稳态介电常数ε∞各自的贡献。

图1 德拜模型

　　介质的极化除Debye模型以外，还有Colo-Colo模型、Lorentz模型及Drude模型等，分别见式(5)～式(7)

　　式中εr0为零频率时的介电常数;m为高频率介电常数与零频率介电常数之比;c为频率常数;τ为时间常数，与温度有关。

　　路面材料复合介电常数也有一定的频率依赖性，但其固态、气态、液态三相的频率依赖程度以及在雷达电磁波频率范围内哪一相介质的频率依赖性占主导地位也需要详细研究。

2、结论

　　总体而言，复合介质介电常数模型虽然不少，但大都是基于一定假设，是在特定情况下才能成立的模型，多用于土壤学和地球物理方面来描述天然地物，其模型建立的最初并非针对路面材料。由于路面材料不同于岩石、土壤等自然界物质，有其自身的材料及结构特点，因此，有必要在充分考虑介质介电常数的频率依赖性以及环境温度对其影响的基础上，深入系统地研究路面材料的介电常数模型。