固定球阀密封比压分析

1、概述

　　COSMOSWORKS是完全整合在SOLIDWORKS中的设计分析系统, 它提供压力、频率、约束、热量和优化分析等, 为设计人员在SOLIDWORKS的环境下, 提供了比较完整的分析手段。本文以固定球阀的阀座为重点研究对象, 因为在阀座的工程设计过程中, 阀座密封面上总作用力及密封比压的计算在实际设计中使用的是经验或修正公式, 利用现有手段, 这两种参数不易准确测出。通过应用COSMOSWORKS有限元分析软件计算模拟工况下固定球阀的密封比压, 并与理论的计算公式进行对比, 为阀门的设计提供了相对准确的参考。

2、实体建模

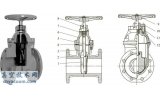
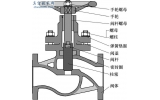
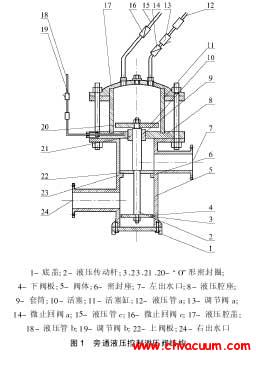
　　以DN239mm, PN25MPa的固定球阀设计为例。在SOLIDWORKS中首先对固定球阀的各个零部件进行实体建模, 并对各零部件进行组装(图1) 。对装配体进行干涉检查, 得到各零件之间无干涉的装配体。

图1　球阀实体建模

3、有限元分析

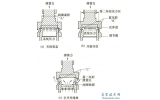
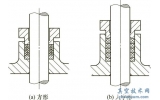
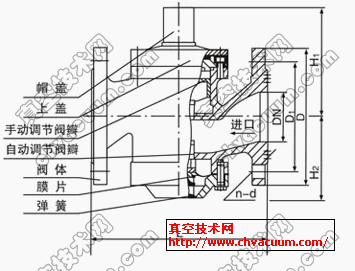
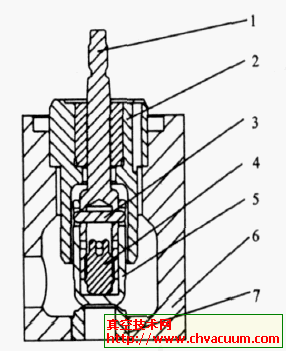
3.1、密封机理

　　固定球阀采用进口密封(图2),此时球阀压差(P-P1) >0(P、P1为阀前和中腔的流体压力)。当压差大到一定程度,即在密封副表面造成一定的压紧比压时, 此比压将引起阀座弹塑性变形, 填塞密封面上的微观不平度以阻止流体从密封副间通过。当压差较小或阀座采用金属材料制作时,依靠压差不能达到完全密封, 此时必须另加一个密封外力, 以加大压紧比压。根据工作压力计算密封所需的必需比压qb 的经验公式为qb = 1.2PN= 30MPa。为保证球阀密封可靠, 在球体和阀座的接触表面上应有足够的比压, 但不得超过密封副材料的许用比压[q]。理论密封比压q1为

图2　球阀密封原理

q1 =Q/S

　　式中Q———球阀密封力, N

　　　　P———公称压力, MPa
　　　　S ———阀座密封面的面积(S = 7634) , mm2
　　　　d2 ———阀座支撑圈外径( d2 = 290) , mm
　　　　D2 ———阀座的外径(D2 = 270) , mm
　　　　D1 ———阀座的内径(D1 = 256) , mm
　　代入各值, 得出q1 的值为40.17MPa。

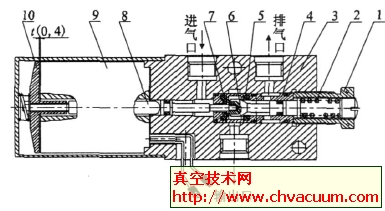
3.2、有限元计算

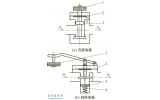
　　由于密封比压的计算过程仅与球体、阀座和阀座支承圈等零部件有关, 所以对其有限元分析模型做了简化(图3) , 这样不仅节约了计算机资源,而且提高了计算结果的准确性。通过模拟现实工况, 需计算得出阀座支撑圈与左右体相接触的面上的压力值Qs。

式中Q1 ———预紧力在阀座支撑圈与左右阀体相接触的面上的压力, MPa
　　Q2 ———公称压力在阀座支撑圈与左右体相接触的面上的压力, MPa
　　S1 ———阀座支撑圈与左右阀体接触面的面积( S1 = 21189.26, 可在SOLIDWORKS中直接测得) , mm²
　　d1 ———阀座支撑圈的内径( d1 = 239) , mm

　　代入各值, 得Qs 的值为23.01MPa。

　　根据现实工况, 在COSMOSWORKS中建立一个静力学分析算例, 并确定约束载荷条件(①固定球体与上阀杆和底盖相接触面。②限定阀座和阀座支撑圈只能在轴向上运动。③将Qs 施加在阀座支撑圈与左右阀体相接触的面上, 进行网格化。④确定球体和阀座支撑圈的材料为35号钢, 阀座的材料为奥氏体不锈钢, 密封面间无滑动(奥氏体不锈钢的许用比压[q] 值为150MPa) , 点击运行, 计算结果如图3c所示。

(a) 分析模型　(b) 模型网格化　(c) 模型计算结果

图3　有限元分析

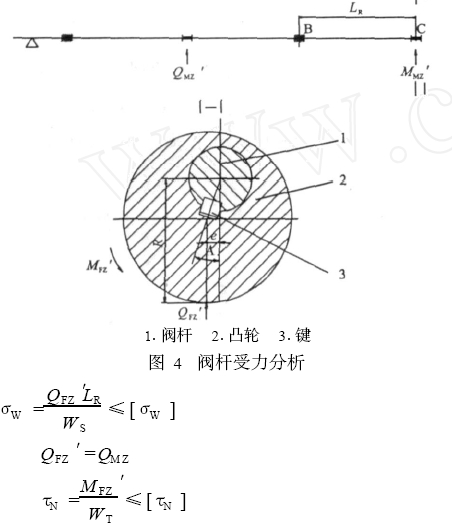
3.3、提取结果

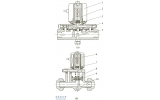
　　在阀座密封面上等距获取25个点(图4) , 然后沿X方向依次探测这25个点的压力值, 再将探测数据导入Excel中进行分析(图5) , 得到密封比压在阀座密封面上呈抛物线分布, 其最大值处于阀座的内径处, 为62.1MPa, 最小值处于阀座中部,其值为40.16MPa。结合阀门密封设计参数必须比压qb(30MPa) 和阀座材料的许用比压[q](150MPa) 。密封比压的值处于qb 和[q]之间,满足了设计准则。

图4　在阀座上取点　　图5　密封比压在阀座密封面上沿X方向的压力分布

4、结语

　　由于在密封过程中, 阀座与球体密封面相对固定, 不能运动, 故在受到预紧力和流体压力后, 密封环的内径轴向相对于中部变形裕量小, 受到的挤压力较大。密封环的径向相对于中部变形裕量大,受到的挤压力也相对较小。另外, 虽然球体与阀座接触, 但由于毛细现象而有流体介质存在, 当球体沿流向有相对运动时, 球体与阀座更加紧密接触,从密封面边缘到中部的流体介质越来越少, 所以密封面边缘处在介质与球体的双重作用下, 受力略大于密封面中部。因此, 在密封面上密封比压呈抛物线分布。在边缘环面, 由于受预紧力、介质施加力和金属球体综合作用, 故产生有波动的变化曲线,尤其在密封面外径处影响更大。由于毛细现象的影响, 取密封面中部的密封比压作为整个固定球阀的密封比压是合理的。根据图5取得密封面中部的压力值为40.16M Pa, 而理论计算的密封比压值为40.17M Pa。两者之间的差值为0.01M Pa, 误差<3%。可见用有限元计算得出的固定球阀的密封比压的值是可信的。而且可以完全反映出密封比压在整个阀座上的分布情况, 从而对整个阀门的设计提供了可靠的设计依据。