高温高压核电闸阀流固热耦合分析
以高温高压核电闸阀为研究对象,分析了流固热三场耦合的原理。数值模拟后得到流体的压力、速度和温度分布,以及闸阀的变形和应力分布。通过对闸阀施加载荷,分析压力和温度对闸阀性能的影响。模拟结果显示,流体在阀座部位产生压力波动,并在底部产生涡流,流体压力能转换成热能。在不限制闸阀整体自由变形的情况下,因热产生的变形较大,因流体压力产生的应力较大,热变形能减小闸阀因流体压力作用而产生的应力。
1、前言
流固热耦合是指在由流体、固体和温度场组成的系统中三者之间的相互作用,流固热耦合问题是流动、应力、温度三场同时存在时的基本问题。流固热耦合问题不仅仅是在流固耦合问题上附加一个体现温度变化的条件,而是将体现流体流动、固体变形、温度场变化的量如流体压力、固相质点位移、绝对温度同时视为基本变量,基本变量处于平等地位。在流固热耦合问题中,热效应与流体压力导致固体变形,固体变形与流体流动导致温度场变化,固体变形与热效应导致流动特性的改变,以上3种效应是同时发生的。
闸阀主要作为接通或切断管道中的介质用,即全开或全闭使用。在核电站中,闸阀受到高温高压流体的作用,必然会产生变形及应力。为了防止全开时闸阀变形或应力超过许用值而造成的结构破坏,必须对其进行计算。由于闸阀工作时结构的变形很小,对流体流动状态及温度的变化影响也很小,故此处只考虑流体压力及温度对闸阀结构的影响,即单向耦合作用。
2、耦合场分析原理
2.1、流固耦合计算
流固耦合是指固体在介质载荷作用下会产生变形或运动,变形或运动又反过来影响介质,从而改变介质载荷的分布和大小。
流固耦合的有限元方程为:

各系数矩阵由全域各单元相应的系数矩阵按统一的方式叠加而成,即:

式中 M———质量矩阵;C———阻尼矩阵;K———刚度矩阵;U、P———由全域各节点所组成的列矢量;Ae———质量矩阵;Be———对流矩阵;Ce———压力矩阵;De———损耗矩阵;Ee、Fe———体积力矩阵;Ge———连续矩阵;He———边界速度矢量;δ、δ、δ———加速度、速度、结构应力列向量。
2.2、温度场分析原理
温度场是指在指定区域内,各个部分的温度分布情况,它是各个时刻物体中各点温度分布的总称。固体与流体本身产生导热现象,流体与固体之间将产生对流换热现象,其原理主要是传热学中的传热基本定律。
(1)热传导微分方程
在笛卡尔坐标系中,对于导热物体中的任意点(x,y,z),三维非稳态导热微分方程的一般形式为:
式中 ρ———密度,kg/m3;cp———比热容,J/(kg·K);λ———导热系数,W/(m·K);![]() ———单位体积发热率
———单位体积发热率
(2)热对流微分方程
连续性微分方程:
运动微分方程:

能量微分方程:

3、闸阀三维实体模型的建立
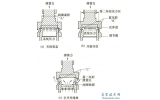
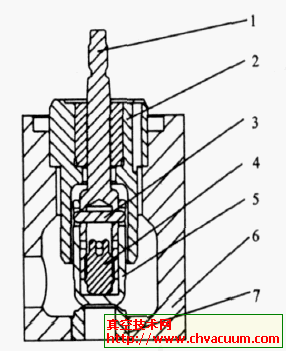
闸阀的三维实体模型要能准确地反映结构的实际情况,同时在保证计算精度的前提下,模型应尽可能简化。闸阀的承压边界主要包括阀体、阀盖和闸板,从力学特性上分析,可以认为阀体、阀盖和闸板作为一个整体来承受内压。因此,在建立有限元模型时,将阀体、阀盖和闸板作为一个整体进行建模,忽略它们之间的连接螺栓。简化处理一些不影响闸阀总体性能的特征,忽略一些不必要的倒角,得到计算模型如图1所示。

图1 闸阀三维实体模型
4、流体流场及温度场分析
4.1、流体流场分析
采用ANSYSWorkbench平台中的CFX对介质流动状态进行分析,阀体内部空腔结构复杂,流体域采用非结构化网格进行离散,划分后得到网格单元数为3058808。对流体进口施加25MPa的压力及330℃的温度值,出口设置outlet,相对压力为0Pa,闸阀壁面采用无滑移固壁条件。图2和图3所示为设计工况下闸阀内流场对称截面上的静压及绝对速度分布。

图2 流场对称截面的静压分布

图3 流场对称截面的绝对速度分布
由图可知,流体最大静压力为13.33MPa,在阀座部位产生压力波动,并在底部产生涡流,这是由于阀座部位的截面形状相对于管道来说产生了突变,导致流体质点之间的相对速度发生变化,质点之间互相混杂、撞击加剧。阀座部位之后静压值明显下降,流道壁面处流速减小。闸阀中腔上部的压降和速度都很小。
4.2、流体温度场分析
由于流体的流动速度很快,其温度下降的趋势很小。由图4可知,在流动过程中,流体的温度值约为330℃(603K),变化值很小,阀座部位之后的壁面底部温度值略有升高,这是由于此处产生涡流,流体压力能转换成热能造成的。

图4 流场对称截面的温度分布
5、闸阀温度场及应力场分析
5.1、闸阀温度场分析
闸阀主要由阀体、闸板、阀杆、阀盖、填料等部件组成,它们均会承受流体的压力和温度载荷。热源是求解温度场的重要边界条件,闸阀温度场的热源是流体。
将流体的温度载荷作用在闸阀的内壁面,外壁面暴露在空气中,对外壁面施加相应的对流换热边界条件。计算后得到闸阀的温度场分布如图5所示,主要承压部件的温度值均在322~330℃。闸阀上部由于距内壁面较远,温度梯度比较明显。

图5 闸阀的温度分布
5.2、闸阀应力场分析
为研究流体压力,温度以及两者的组合各自对闸阀的影响,下面将对其分别进行计算。
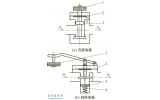
(1)将流体压力载荷作用在闸阀内壁,对阀体主通道两端面施加20MPa的接管载荷。考虑到与阀门所连接的管道比较长,轴向伸缩量相对于阀门比较大,而且管道与阀门通道具有几乎相同的径向伸缩量,故对阀门左端面施加无摩擦约束且固定端面下方的一点。计算后得到图6所示的只有流体压力载荷而没有温度载荷的闸阀变形图6(a)及应力图6(b)。闸阀有沿流体流动方向变形的趋势,最大变形为19μm,位于阀门出口端。闸阀的最大应力为185.2MPa,出现在闸板与阀体导向键的配合处,此处结构复杂,容易产生应力集中。

图6 有压力无温度载荷时闸阀变形和应力
(2)将流体温度载荷作用在闸阀内壁,接管载荷及约束条件与(1)相同,计算后得到图7所示的只有流体温度载荷而没有压力载荷的闸阀变形图7(a)及应力图7(b)。闸阀有以固定点为中心点向周围放射状膨胀的趋势,最大变形为2.9mm,位于阀杆顶端。闸阀的最大应力为64.39MPa,出现在闸板与阀座的配合处,此处结构受热后膨胀受到限制,容易产生应力集中。

图7 有温度无压力载荷时闸阀变形和应力
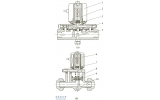
(3)将介质压力和温度载荷同时作用在阀门的内腔壁面,对其进行单向流固热耦合计算,接管载荷及约束条件与(1)相同。计算后得到阀门在开启状态的变形及应力分布如图8所示,阀门最大变形为约2.9mm,位于阀杆顶端。最大应力为173.3MPa,位于闸板与阀体导向键的配合处。

图8 单向流固热耦合时闸阀变形和应力
6、结论
(1)由于流道截面积在阀座部位产生变化,流体在此处产生压力波动,并在底部产生涡流,减小阀座部位流道截面积的变化能减小涡流损失;
(2)由于流体的流动速度快,在流经闸阀的过程中温度下降的趋势很小。阀座部位产生涡流,流体压力能转换成热能使壁面底部温度升高;
(3)在不限制闸阀整体自由变形的情况下,与流体压力相比,因热产生的变形较大,而应力较小,热变形能减小闸阀因流体压力而产生的应力。