热风炉阀声振耦合有限元分析

　　为了减小热风炉阀在运行时噪音对周围居民的影响，运用有限元分析软件ANSYS对某热风炉阀结构及周围声场进行分析。在流体运动管道声场、小孔喷注消音等相关理论基础上，建立了结构、流体、声场有限元模型。通过建模、划分网格、加载、求解以及后处理等步骤，对该阀体及附近区域流体进行声振耦合计算分析。结果表明：带孔板结构在孔径为4mm时，厚度为20mm时，该阀体的结构形式的消音效果比到较理想，能为热风炉阀减噪设计提供一定的参考依据。

　　引言

　　热风炉是钢铁冶炼设备高炉的一个重要组成部分。热风炉的主要作用是把鼓风加热到要求的温度，用以提高高炉的效益和效率。但是在冶炼过程中经常要调节气体流量的大小，以配合各种工况下钢铁的冶炼。为了实现自由调节气流目的，真空技术网(http://www.chvacuum.com/)认为需要用阀或阀组的开启或关闭。其中阀在启闭瞬间产生巨大的噪音，而噪声又已成为威胁人类生存的三大公害之一，噪声对人们的心理和生理都有严重的影响。故需要对阀组进行声学仿真分析，以期能得到阀组的噪音值，从而判定噪声危害的程度，而该噪声产生的主要原因是振动，又由于阀或阀组在此过程中的使用频率高，属于易发生损坏失效的部件，故对热风炉阀做声固耦合分析对减噪和强度校核有着重要的实际意义。

　　笔者以某热风炉阀为研究对象进行声固耦合分析，主要从模态振型和声固耦合等方面对阀体和阀周围区域流体进行分析。重点计算了阀体及阀体周围的声场，得到了阀体周围一定区域内噪音值，以期通过改变结构以达到减噪的效果，并期望此计算结果能对热风炉阀减噪有一定的参考意义。

1、声振耦合有限元分析理论基础

1.1、声学Helmholtz波动方程

　　解决声学外声场问题的最终目的就是要求解某个特定问题的Helmholtz(人名：亥姆霍兹)波动方程的解，而声学Helmholtz方程是结合了声波的连续方程、运动方程和物态方程推导得来的。

　　(1) 式(1)中：k=2πf/c为波数；ω=2πf为角频率；f为频率；λ为对应的波长；为拉普拉斯算子；为声波在流体介质中的传播速度；p(x，y，z)=p0(x，y，z)+p′(x，y，z)为流体的声压；p0(x，y，z)为初始位置流体声压；ρ(x，y，z)=ρ0(x，y，z)+ρ′(x，y，z)为流体的密度；ρ0(x，y，z)为静态声压；q(x，y，z)=q0(x，y，z)+q′(x，y，z)为附加质量；q0(x，y，z)为初始质量。

1.2、耦合声学有限元方程

　　声音作用于结构上的声压载荷可以看作是附加的法线载荷，可得到动力学方程如下：

　　(Ks+jωCs-ω2Ms)·{ui｝+Kc{pi｝={Fsi｝ (2)

　　在流体和结构耦合的位置处，结构法线方向的振动速度与流体法线方向的振动速度相同，在流固耦合交界面处，结构的振动速度可以看作是声音的附加速度输入，这时声学方程变化为如下方程(3)所示：

　　(Ka+jωCa-ω2Ma)·{pi｝-ω2Mc{ui｝={Fai｝ (3)

　　将方程(2)、(3)写成一个矩阵的形式，并进行耦合处理，得到耦合声学方程：

　　(4) 式(4)中：Ks为结构网格上没有受到约束部分的刚度矩阵；Ka为模态中声学刚度矩形；Ms为结构网格上没有受到约束部分的质量矩阵；Ma为模态中声学质量矩形；Cs为结构网格上没有受到约束部分的阻尼矩阵；Ca为模态中声学阻尼矩形.ρ0为静态声压；为激励荷载；ω=2πf为角频率；{pi｝为压力矩阵；为声学激励；{ui｝为固体位移矩阵；ω=2πf为角频率。

2、微穿孔板消声阀体声场计算

2.1、工程阀体概述

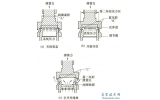
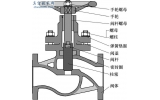
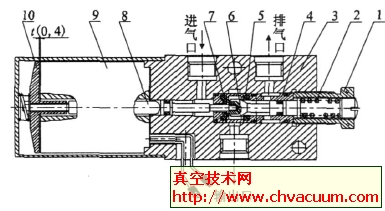
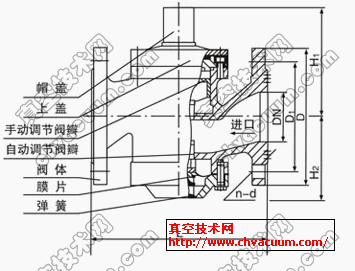
　　图1所示即为某热风炉管道的一个阀体，当气态流体从左端入口流入，随活塞推移而经穿孔柱板流入腔体，该过程中噪音主要源自气体流动时对固体管壁产生冲击而产生的机械振动噪音和气体湍流振动的气动噪音。该阀结构是依据小孔喷流消音机理，小孔喷注消音的设计机理是根据科学院声学研究所马大猷教授等人提出的小孔喷，注噪声极其控制理论，从发声机理上使它的干扰噪声减少，由于喷注噪声峰值频率与喷口直径成反比，若喷口直径变小，喷口辐射的噪声能量将从低频移向高频，于是低频噪声被降低，高频噪声反而增高。经试验表明，当孔径d≤4mm时，人耳能听到的低频噪音能被降低，以达到减噪的作用；同时若在中间部分加入一个活塞来回的滑动，以达到控制流量的效果，故该阀体兼有消音减压的效果。

图1 阀体结构示意图

　　故选用孔径为4mm的穿孔板焊接在热风炉管道中，左端是管道入口，右端是管道出口，中间部分为带孔柱板，气体经左端通过柱板再进入大容积腔体，最后再通过管道出口流出，整个过程既实现了阀体减压的效果，也实现了减噪的效果。

2.2、有限元计算

　　2.2.1、建立几何模型

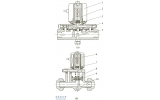
　　建立如图2所示的带孔柱板，其具体尺寸为内径150mm，外径160mm，底板厚度为10mm，然后再在其外围建立一个半径为200mm的实心圆柱体，将实心圆柱体减去带孔柱板，得到如图3的实体流体模型。再在外部建立一个半径为600mm的球形区域用来模拟周围的声场，也即是周围的流体。结构模型如图4所示，其模型透视如图5所示。

图2 带孔柱板图

图3 内部流体

图4 周围声场模型图

图5 线可视模型图

　　2.2.2、建立有限元模型

　　对于三维声学问题，ANSYS(有限元分析软件)声场分析指定了两种单元类型：三维模型的流体部分分别使用Fluid30(ANSYS软件中的一种单元)单元和Fluid130(ANSYS软件中的另一种流体单元)，且Fluid130单元必须和Fluid30一起使用，用来构造包围Fluid30单元的无限外壳。利用两种单元类型可以构造流体部分的模型，然后利用相应的结构单元Solid185构造固体模型。只有Fluid30单元才能与结构单元相接触；Fluid130单元只能与Fluid30单元相接触，而不能直接与结构单元接触.由于ANSYS的以上功能，故分别选用Solid185单元来模拟结构模型，选用Fluid30来模拟与固体接触的流体部分，选用Fluid130单元用来构造无限外壳。

　　结构模型采用普通低碳钢制作，其材料属性分别为弹性模型Ex为2.1×105MPa，泊松比为0.3，密度为7.85×10-9t/mm3，流体模型需要定义速度和密度，速度为3.44×105mm/s，密度为1.21×10-12t/mm3，无限外壳的声速为2×103mm/s。

　　由于柱板有很多小孔，若是不作处理自由划分网格，小孔边缘位置网格质量很差，若是要保证小孔边缘的网格质量，又导致整个柱板的单元数过多而加大计算负担甚至无法计算。故采用Solid185单元对柱板上小孔进行切分之后再进行网格划分，切分之后的柱板结构如图6所示，切分之后对柱板两端和底板进行扫掠划分，然后对有小孔的中间柱板部分采用智能划分，划分网格之后的网格如图7所示。对中间部分的流体采用Fluid30单元智能方式划分，划分之后的网格如图8所示，中间网格局部视图如图9所示。对外围球体部分采用Fluid30单元自由划分，单元尺寸设置为40mm，划分网格图如图10所示。

图6 切分之后模型图

图7 切分之后网格图

图8 中间流体网格图

图9 中间流体网格正视图

图10 中间流体网格正视图

　　2.2.3、加载与求解

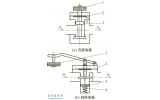
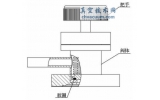
　　划分网格后，由于流体和固体是两个单独的部分，只有通过耦合才能使流体和固体进行有效关联从而实现计算，故在流体和固体交界面处定义流固耦合面，即FSI(流固耦合)如图11和图12所示。然后在柱板入口处施加0.25MPa的入口压力。再在无限外壳面定义吸声属性，此处吸声属性定义为1，即全吸声属性，如图13所示。最后设置计算参数并计算，设置步长为20，范围从500至1000。

图11 流固耦合交界面(整体视图)

图12 流固耦合交界面(局部视图)

图13 无限外壳定义吸声属性

3、声场分析与结论

　　随着人们对其所居住环境越来越重视，环保部门开始慢慢地关注和管制噪音的危害，而且出台了相关限制噪音的标准和规范。工业企业环境标准所允许的最大噪音值为90dB，实际普通热风炉阀在启闭时产生的噪音高达120dB，严重地污染了周围的环境。对该有限元模型求解计算成功后通过后处理，得到如图14所示声压级云图，从该图中可看出最大的声压级值为79.2dB。由此可知采用该新型减压阀能从模拟仿真方面得到的噪音值满足相关法律法规所要求控制的噪音范围，可推知小孔喷注是一种行之有效的减噪方法，但必须要选用合理的小孔孔径及排列方式。

图14 声压级分布云图

4、结语

　　通过对某热风炉系统中阀做声振耦合有限元计算，并分析声场结果，最后可得出以下几点结论：

　　a.进一步从模拟仿真角度论证了小孔喷流是减小噪音的有效途径之一。

　　b.仅当小孔的直径为4mm左右时，消音减噪的效果较佳。若是孔径太小，小孔容易被气体中的杂质堵塞，若是孔径过大，又不能将高频噪音滤去，达不到消音减噪的效果。

　　c.计算过程及计算结果表明，ANSYS是一款比较实用的有限元处理软件，其用户界面良好，前、后处理功能强大，计算精确度高，是求解声场分布行之有效的有限元处理软件。