高压管线固定球阀矩形密封圈有限元分析

2013-09-05 张浩强湖南电气职业技术学院机械工程系

　　利用ANSYS建立了公称通径1500mm，公称压力15MPa的高压管线固定球阀阀座和球体连接处矩形聚四氟乙烯密封圈的二维轴对称模型。在矩形密封圈二维轴对称模型右上线8施加设计比压15.74MPa，分析了矩形圈长度与最大接触压力和位移和的关系。结果表明随长度的增加，最大接触压逐渐增大，但变化不大;变形后的位移和随长度增加而增加，且变化较大;可能出现裂纹的位置在施加压力端近似半椭圆的区域内;矩形密封圈接触压力均匀、密封面大、密封效果好。

　　矩形密封圈以其结构简单和自身特点被应用于一些领域，德国宝色霞板公司和力士乐公司在液压阀的平面各油口处，均采用矩形圈，在我国有杆抽油机井口光杆处的密封98%都采用矩形密封圈[1]。本文利用有限元分析的方法建立矩形密封圈的有限元模型，并分析了矩形圈长度对最大接触压力以及位移和的影响，为合理选择矩形密封圈提供了设计依据。

1、有限元模型的建立

　　1.1、几何模型的建立

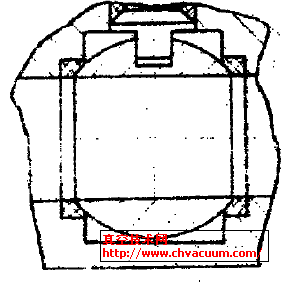
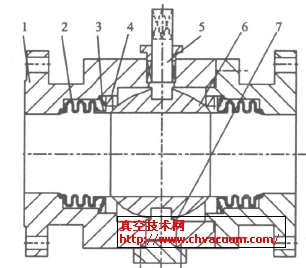
　　将矩形密封圈及密封结构的球体、阀座作为整体进行分析。根据密封结构的几何形状、材料、边界条件的特点，建立矩形密封圈的平面轴对称几何模型如图1所示，根据密封结构特征、选择8节点轴对称单元plane82模拟阀座与球体。采用8节点轴对称单元visco108模拟聚四氟乙烯矩形密封圈，可以较好的描述问题的受力和变形情况，计算结果精度高[2]。

　　1.2、随动强化模型

　　假定在塑性变形过程中，屈服曲面的形状和大小都不改，只是应力空间中作刚性平移，如图2所示。设在应力空间中，屈服面内部中心的坐标用αij表示，它在初始屈服时等于零，于是，随动强化模型的加载曲面可表示为：

F(σij-αij)-k=0。

　　显然F(αij)-k=0为初始屈服曲面，产生塑性变形以后，加载面随着αij而移动，αij称为移动张量。

图1 二维图图2 随动强化

　　1.3、网格划分

　　ANSYS所有的分析都要输入材料的属性。聚四氟乙烯材料为弹塑性材料，采用双线性随动强化材料模型来模拟，参数选取如下：弹性模量E=1.0GPa;屈服强度σy=18MPa;屈服应变ey=1.6%;切向模量et=0.12GPa;泊松比μ=0.4。球体E=206GPa，泊松比μ=0.3;网格划分与约束条件使用网格工具中的smartsize智能网格划分工具进行网格划分，对矩形密封圈设定划分精度为1，对阀座和球心设定划分精度定为2;系统将自动根据模型的形状和尺寸，模型局部的曲率、线与线之间的距离。以及所设置的精度级别，自动选择合适的网格密度进行划分[3]。如图3所示。

　　1.4、接触对的生成

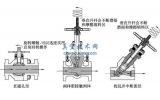
　　在制作模型时按变形前的实际工况造型。定义接触类型为面面接触，摩擦系数为0.137。模型中包含3个接触对：一是球面与矩形密封圈左下面的接触对;二是阀座左上面与矩形密封圈左上面的接触对;三是阀座右下面与矩形密封圈右下面的接触对。球面与矩形密封圈左下面的接触对在3个接触对中作为主接触面，其它两个接触对为从接触面。对矩形密封圈采用8节点conta171单元，阀座与球面选用targe169单元[4]。结构如图4所示。

图3 划分网格后的模型图4 密封接触面法向

　　1.5、边界条件与加载方式

　　设置边界条件和受力模型，约束阀座与球体的所有自由度，组装时，由于在阀座传递过来的压力的作用下，施加作用力给矩形密封圈右上面，通过对矩形密封圈的挤压，产生形变，达到密封的作用。根据以上原理，在加载时，由于采用的是轴对称结构，矩形密封圈右上面的那根线，线号为8，给线8施加15.74MPa载荷，然后运算。如图5箭头所示。

　　1.6、求解

　　有限元法就是将连续体用有限个节点和单元划分成离散体，然后建立每一个单元体的有关公式，将它们在离散点处结合起来，得到整个物体的平衡方程组。设置时间为2，子步数为10，最大的子步数为1000，最小的子步数为10，打开大变形效应，进行求解运算。

图5 施加压力图

2、计算结果与分析

　　2.1、长度对接触压力与位移和的影响

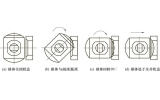
　　从图6到图9可以看出，在矩形圈长度为65mm、70mm、75mm、80mm时，最大接触压力均大于工作压力，可以保证密封，而最大接触压力变化不大，从表1可以看出，矩形圈变形后的位移和随长度增加而增加，在70mm时压缩率最小为6.7%，且最大接触压力为17.2MPa，所以选择矩形圈长度为70mm进行密封计算。

图6 65mm时最大接触压力17MPa

　　2.2、阀座与球体的接触分析

　　从图11可看出，在施加压力15.74MPa时，位移和最大为4.586mm，即为矩形密封圈端面被压缩量，从而为正确设计矩形密封圈沟槽的尺寸提供依据，矩形密封圈X方向的最大应力11.9MPa大于Y方向的最大应11.4MPa，且都在许用应力范围内。

图7 70mm时最大接触压力17.2MPa

图8 75mm时最大接触压力17.3MPa

图9 80mm时最大接触压力17MPa

图10 以力F为基础的收敛图

图11 位移和4.586mm 图12 X方向应力11.9MPa

图13 Y方向应力11.4MPa 图14 VonMises应力14.9MPa

图15 接触面上的接触压力分布图

　　范.米塞斯(VonMises)应力σe为：

　　式中：σ1、σ2、σ3为单元体3个方向的主应力。范-米塞斯应力反应了矩形密封圈截面上各主应力差值的大小[5]。一般来讲，应力值越大的区域，材料越容易出现裂纹。此外，应力越大，将加速聚四氟乙烯材料的松弛，从而造成“刚度”下降。在图14中可能出现裂纹的位置在施加压力端近似半椭圆的区域内。

　　密封面上密封比压分布如图15所示，可以看出：密封比压分布十分有规律，沿密封面中心向两侧逐步减速小，最大比压值在图中红色部份为17.5MPa，大于工作压力15MPa，小于密封面许用比压39MPa，可以保证密封。固定球阀的密封比压理论解相对于密封面上的密封比压整体而言值偏小，这是因为密封面密封比压从中心到两侧逐步减小，理论解是由密封面平均直径得出，故其值偏小。用有限元分析法求解密封面密封比压的过程虽然相对比较复杂，但若经过合理的建立模型和设置边界条件，就能够得出比较真实的密封比压值，在工程上容易实现。

　　从矩形密封圈的位移和最大为4.586mm可以看出，聚四氟乙烯矩形密封圈长度为70mm，压缩率为6.5%就可以产生最大17.2MPa的密封比压，矩形圈在很小压缩量的情况下就可实现密封。矩形密封圈接触压力均匀，密封面大，密封效果好[6]。

图16 最大VonMises应力节点2798与时间的迭代关系图

图17 X方向的位移最大节点2752与时间的迭代关系

　　图16为矩形密封圈X方向VonMises应力最大的节点2798的时间历程图，呈线性增长，沿X负方向最大VonMises应力值为0.1458E8Pa。

　　图17为阀座上沿X方向变形最大的节点2752在ANSYS时间历程后处理器中的变形时间图，可以看出，位移呈非线性变化，这是因为矩形密封圈的压缩反力呈非线性增加，曲线在压缩过程中出现跳跃拐点[27]，曲线在压缩过程中出现跳跃拐点，这是由于矩形密封圈为平面与球面接触，刚施加压力时，平面垂直于球面法向移动，而后平面两端弯曲与球面接触，矩形密封面受压弯曲失稳，受力结构位置突然改变造成的。且压缩位移越大，压缩反力增加的越快，从而最大节点位移变形减小。

3、结论

　　本文采用双线性随动强化材料模拟矩形密封圈，刚体材料模似阀座和球体，建立有限元模型，材料常数正确，网格划分合理，通过设置合理的边界条件及施加载荷，较好的进行了接触分析。得出矩形密封圈长度与接触压力及位移和的关系，为在实践中合理选择矩形密封圈提供了理论依据。通过对VonMises应力的分析，得出矩形密封圈可能出现裂纹的区域。并对X方向变形最大的节点进行了时间历程后处理，对位移出现的非线性变化进行了分析，在压缩过程中出现的跳跃拐点是由于矩形密封圈受压弯曲失稳造成的。有限元的理论分析与实践相符，在以后的工程应用中可以加大聚四氟乙烯矩形密封圈的应用。