一种新型蝶阀调节特性的研究

　　阐述了在普通蝶阀的基础上，加设适当几何结构配流板的方法，使普通蝶阀具有线性流量特性，并用数值模拟计算出阀门的流量特性。然后搭建实验平台，验证了阀门的流量特性，结果表明该流量控制阀具有良好的线性调节功能和高精度的流量控制。

　　在工程中，线性流量特性调节阀的优点是单位行程的变化所引起的流量变化是不改变的，在解决供热、空调系统中的水力失调、冷热不均等问题上得到了广泛的运用。现有的线性调节阀一般为座阀，但现有的座阀会使管道内流动阻力增大，造成能量损失较为严重。“十二五规划”国家提出了明确的节能计划，为了大力推广国家提出的节能减排计划笔者设想在蝶阀阀板上安装能实现线性流量特性的配流板，使这种新型的蝶阀具有线性流量特性和结构简单，流动阻力小，流通能力大等优点。

1、阀体的创新设计

　　阀门流量公式：

(1)

　　式中：Qs为设定流量，ΔP为阀门两端的压差，Kvs为流量系数，θ为阀门开度，θmax为阀门最大开度。

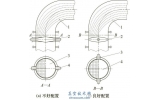
　　阀门的流量能力与阀芯的通流面积有对应的关系，即阀门的开度决定阀门的通流面积，为了获得阀门的线性流量特性，希望设计的阀门的通流面积与开度呈线性关系，因此对阀芯进行合理机械结构设计是获得线性流量特性的关键。根据以往积累的经验，设计对称折板阀芯结构，如图1所示。

图1 对称折板阀芯示意图

　　其中通流面积的算法，采用面积投影的方法进行计算。其结构几何参数包括：折板高度、折板宽度、折板相对位置(折板夹角始终保持直角)。其中折板的特殊位置使得折板相对位置与折板的宽度耦合，即此阀芯的结构参数为2个：折板高度和折板宽度，阀门的通流面积取决于这2个参数，通流面积的计算公式如下：

(2)

　　式中：A为通流面积;R为管道半径;a为x坐标上某位置，随阀门开度变化取不同值;L为折板宽度;H为折板高度;θ为阀门开度。

　　分别选取不同的折板高度和折板宽度计算通流面积与阀门开度的关系，找到合适的尺寸参数，选取适当阀芯尺寸以实现阀门的线性流动特性，文中采用的管道取不同折板高度H和折板宽度L时，通流面积随相对开度变化的曲线如图2所示。

图2 不同折板阀体的开度与通流面积的关系

　　对比每组的阀门开度与通流面积的关系数据，选取最接近线性关系的参数作为折板的结构尺寸，即选择折板宽度为8mm，折板高度10mm。

2、数值计算

　　采用工程中应用比较广泛的RNGκ-ε三维湍流模型和非结构化网格的SIMPLE方法。对不同阀门开度θ、不同来流速度条件下的阀门内流场分布进行了数值模拟，入口采用速度入口边界条件;出口采用自由流边界调节，收敛条件为速度和湍流的残差值均小于0.0001。

　　计算结果收敛后，通过对阀前2D～阀后5D的管道截面的压力场和速度场进行分析，得到阀前、阀后截面压力等值线云图，如图3、图4所示。

图3 阀前截面压力等值线云图

图4 阀后截面压力等值线云图

图5 对称折板模型相对开度与相对流量系数

　　关系曲线-数值模拟结果

　　图5中，对称折板模型从30°～90°共7种开度下的流量系数值具有良好的线性特性。通过线性拟合，得到拟合曲线方程为：

(3)

3、实验研究

　　为了验证数值模拟的计算精确度问题，论文专门搭建了实验测试平台，实验装置如图6所示。

图6 实验装置图

　　通过调节旁路调节阀来改变被测蝶阀两端的压差，利用计算机快速数据采样和信号处理得到通过蝶阀的流量Q两端压差ΔP以及其他实验数据，如表1所示。

表1 阀门不同开度下的实验数据(流量：m³/h;压差：kPa)

　　拟合数据，得到实验流量特性公式如下：

(4)

　　在相对开度0～1的范围内，对比两实验数据和数值模拟数据可得两者最大相对误差为4.6%，满足设计目标流量误差低于5%的要求，可见误差在可接受范围内。将模型的数值模拟流量特性曲线和实验测量流量特性曲线进行比较，结果如图7所示。

图7 阀门流动特性曲线的数值模拟和实验测试数据对比

　　由图7可知，折板配流板的线性流量特性改善了普通蝶阀在大开度范围调节时流量变化缓慢的缺点。同时，维持了蝶阀在小开度范围调节时较好的线性流量特性，数值模拟和实验所得的流量特性曲线线性度都较好，相互之间差值较小，这说明以通流面积曲线作为参考，设计蝶阀配流板的可行性。也说明了折板状配流板，可以使普通蝶阀获得线性的流量特性。

4、结论

　　该文介绍了添加折板状配流板进行优化设计的方法，此种折板状配流板不仅加工制造较为简便，同时使蝶阀的通流面积在大开度条件下的变化率增大，实现比较理想的线性流量特性。

　　实验研究表明这种控制蝶阀产品具有理想的线性流量调节特性，在调节精度、调节范围方面都有明显的改进和提高，论文成果在工程中有重要的应用价值。