三偏心蝶阀密封面联动磨削的运动特性分析

2013-09-08 陈军苏州纽威阀门股份有限公司

　　三偏心蝶阀密封面的形状尺寸和表面质量是影响其密封性能的关键要素，密封面的高质量加工一直也是各厂家的难点。在传统的空间几何理论分析基础上以阀体密封面的联动磨削为研究对象，阐述了砂轮与工件的运动特性关系。

一、前言

　　三偏心蝶阀作为一种高性能阀门，在各个行业应用越来越广，对其密封面的质量要求也越来越高，密封面的高质量加工一直是国内行业中的难点，各企业对三偏心蝶阀密封面的磨削方式基本上还处于摸索阶段，尤其是联动磨削在国内基本上没有成功的案例。

二、密封面成形分析

　　由于三偏心蝶阀密封面形状的特殊性，密封面为一个圆锥的斜截面，传统的研磨方法在其上都不易实现，对密封面的最终成形国内的厂家基本上都是采取的车削方式。车削加工的局限性致使了产品性能无法进一步提高，研究新的磨削设备与磨削方式，提高产品的密封性能一直是各个厂家正在研究的课题。

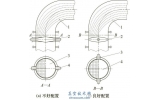
　　以下列举了四种密封面成形的磨削方式，如图1所示。从图中可以看出四种磨削运动过程各有特点。图1a为采取成形砂轮，砂轮面完全覆盖磨削轨迹，磨削过程为砂轮旋转运动的同时进行横向进给。图1b同样为采取成形砂轮，砂轮面略大于阀体密封面宽度，磨削过程为砂轮旋转运动，同时沿密封面圆锥母线进行上下运动(角度插补)，并进行横向进给。图1c为采取传统平行砂轮，砂轮主轴旋转一定角度(密封面圆锥母线平行)，砂轮面覆盖磨削轨迹，磨削过程为砂轮旋转运动，并进行横向进给。图1d为同样采取传统的平行砂轮，砂轮主轴旋转一定角度(密封面圆锥母线平行)，砂轮面略大于阀体密封面宽度，运动过程为砂轮旋转运动，同时砂轮沿圆锥母线上下运动并与密封面同步(即运动过程中砂轮面不脱离阀体密封面)，并进行横向进给，即砂轮与工件进行联动磨削。四种磨削方式各有其优缺点，同时对机床的要求也各不相同。图1a到图1c的运动过程相对比较简单。图1a与图1c密封面的最后成形完全取决于砂轮面本身的形状，同时在磨削过程中工件对砂轮的反作用力的着力点时刻在变化，砂轮主轴容易疲劳破坏。图1b在磨削过程中为断续磨削，存在冲击，砂轮主轴容易疲劳的同时阀体密封面的成形也不是很好。图1d为砂轮与工件进行联动磨削，没有图1a到图1c的影响，砂轮主轴受力恒定且不存在冲击。但是要完成此联动磨削，并不容易，一是对机床的要求比图1a到图1c的要高，机床c轴(工作台主轴)能准确定位，且能与z轴能建立联动关系，同时机床b轴(主轴的旋转轴，即形成β角)定位准确。二是联动运动相对复杂，完成联动数控编程必须要有明确的几何数学关系。所以求解砂轮移动速度v与工件的旋转角度θ的几何数学关系是完成联动磨削的必要条件。所以以下着重对图1d的联动磨削运动特性进行分析研究。

(a)磨削方式1 (b)磨削方式2

(c)磨削方式3 (d)磨削方式4

图1 密封面成形的磨削方式

1.斜模2.工装定位板3.阀体4.砂轮

三、砂轮与阀体密封面联动运动特性分析

　　取图1d中的密封面最低点为研究起始点，为了便于研究砂轮的运动方程，以圆锥中心线为z轴，密封面的最低点所在的平面为xy平面，且最低点在x轴上，建立坐标系，如图2所示。H为圆锥的高度，R为圆锥的底半径，即密封面最低点到工件旋转轴z轴的距离。△ACC1为斜模平面，∠OAC=α(斜模角)，∠AMO=β(圆锥半锥角)，弧ABC为斜模平面与圆锥面的交线，即为砂轮运动轨迹(也为阀体密封面)。△MOB1为工件(或C轴)从初始点旋转角度q时所在的位置。旋转角度q所用时间为t，则动点b为此时的砂轮位置。假定动点B在z轴上的投影为B2，则B点到z轴的动半径R(θ)=BB2，B点在z轴上的投影高度z(θ)=OB2。令B点在x与y轴方向的坐标分别为x(θ)与y(θ)，则R(θ)=[x(θ)2+y(θ)2]。令M(θ)为砂轮在圆锥母线B1M方向位移，v为砂轮在圆锥母线B1M方向上的速度，ω为工件旋转角速度，由几何关系可知：

　　实际的加工过程中，R、ω、α和β均为已知常数，所以v=v(θ)，对其用MATLAB进行计算分析得出其v—θ曲线如图3所示，从v—θ曲线图中可以看出，v与θ是非线性关系，而是速度v相对工件旋转角度θ成正弦规律变化。明确了两者之间的真实关系之后，便可为数控编程提供正确联动数学模型，使联动磨削得以实施。